题目内容
16．
古代的铜钱在铸造时为了方便细加工，常将铜钱穿在一根木棒上，加工时为了较好地固定铜钱，将铜钱当中开成方孔，于是人们也将铜钱称为“孔方兄”．已知图中铜钱是直径为3cm的圆，中间方孔的边长为lcm，若在铜钱所在圆内随机取一点，则此点正好位于方孔中的概率为（ ）| A． | $\frac{4}{9π}$ | B． | $\frac{9π}{4}$ | C． | $\frac{4}{3π}$ | D． | $\frac{3π}{4}$ |
分析 求出铜钱面积的大小和中间正方形孔面积的大小，然后代入几何概型计算公式进行求解．
解答 解：如图所示：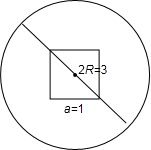
∵S正=1，S圆=π（$\frac{3}{2}$）2=$\frac{9π}{4}$，
∴P=$\frac{{S}_{正}}{{S}_{圆}}$=$\frac{4}{9π}$．
则点正好落人孔中的概率是 $\frac{4}{9π}$，
故选：A．
点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=$\frac{N（A）}{N}$求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，∠BAC=$\frac{2π}{3}$，圆M与AB，AC分别相切于点D，E，AD=1，点P是圆M及其内部任意一点，且$\overrightarrow{AP}$=x$\overrightarrow{AD}$+y$\overrightarrow{AE}$（x，y∈R），则x+y的取值范围是[4-2$\sqrt{3}$，4+2$\sqrt{3}$]．
4．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，8，13…．该数列的特点是：前两个数都是1，从第三个数起，每个数都等于它前面两个数的和，人们把这样的一列数组成的数列{an}称为“斐波那契数列”，则a2016a2018-（a2017）2等于（ ）
| A． | 1 | B． | -1 | C． | 2017 | D． | -2107 |
8．函数f（x）=（x+1）ex的图象在点（0，1）处的切线方程为（ ）
| A． | x-y+1=0 | B． | 2x-y+1=0 | C． | ex-y+1=0 | D． | 2x+y-1=0 |
5．已知点A（1，-2），若向量$\overrightarrow{AB}$与$\overrightarrow{a}$=（2，3）同向，|$\overrightarrow{AB}$|=2$\sqrt{13}$，则点B的坐标为（ ）
| A． | （4，6） | B． | （-4，-6） | C． | （5，4） | D． | （-5，-4） |