题目内容

一般的一个屋顶的某一斜面成等腰梯形，最上面的一层铺了瓦片21块，往下每层多铺一块，斜面上铺了瓦片19层，共铺瓦片的块数
 
．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的定义知，每层铺的瓦片数是以21为首项、以1为公差的等差数列，利用等差数列的前n项和公式求出斜面上铺了瓦片19层共铺瓦片数．
解答： 解：由题意知，每层铺的瓦片数是以21为首项、以1为公差的等差数列，
所以斜面上铺了瓦片19层，共铺瓦片的块数s=19×21+
19×18
2
×1=570，
故答案为：570．
点评：本题考查等差数列的实际应用，等差数列的前n项和公式，属于基础题．
练习册系列答案
相关题目
命题“若x2=0，则x=0”的否命题是
 
．
函数y=
-x2+2x+3
的定义域是
 
．
函数f（x）=2sin（2x+φ）（|φ|＜
π
2
）的图象向左平移
π
6
个单位后关于原点对称，则函数f（x）在[0，
π
2
]上的最小值为（　　）
A、-1
B、-
3
C、1
D、
3
复数
1
1-i
+
3-2i
2+3i
在复平面内对应的点到原点的距离为
 
．
设向量
a
，
b
不共线且k
a
-
b
与
a
-k
b
共线，则实数k的值为（　　）
A、1B、-1C、1或-1D、0
已知集合A={x|lgx≤1}，B={x|2x≤1}，则A∪B等于（　　）
A、（0，10]
B、（-∞，0]
C、（0，+∞）
D、（-∞，10]
已知函数f（x）=lg
1-x
x+1
（-1＜x＜1）．
（1）判断f（x）的奇偶性；
（2）证明f（x）是区间（-1，1）上的单调减函数；
（3）求函数f（x）的值域．
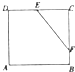在如图所示的边长为6的正方形ABCD中，点E是DC的中点，且
CF
=
2
3
CB
，那么
EF
•
AE
等于（　　）
A、-18B、20
C、12D、-15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网