题目内容
 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB,BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB,BB1的中点.(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=1,AB=
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连结AC1交A1C于点F,则F为AC1中点,可得BC1∥DF,利用线面平行的判定定理,即可证明BC1∥平面A1CD;
(2)证明CD⊥平面ABB1A1,DE⊥A1D,转换底面,即可求三棱锥D一A1CE的体积.
(2)证明CD⊥平面ABB1A1,DE⊥A1D,转换底面,即可求三棱锥D一A1CE的体积.
解答:
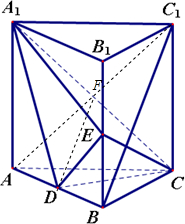 (1)证明:连结AC1交A1C于点F,则F为AC1中点.
(1)证明:连结AC1交A1C于点F,则F为AC1中点.
又D是AB中点,连结DF,则BC1∥DF
(2)解:∵ABC-A1B1C1是直三棱柱∴AA1⊥CD
∵AC=CB,D为AB中点,
∴CD⊥AB,
∵AA1∩AB=A,
∴CD⊥平面ABB1A1,
∴AA1=AC=CB=1,AB=
,
∴∠ACB=90°,CD=
,A1D=
,DE=
,A1E=
,
∴A1D2+DE2=A1E2,∴DE⊥A1D,
∴VD-A1CE=VC-A1DE=
×(
×
×
)×
=
.
 (1)证明:连结AC1交A1C于点F,则F为AC1中点.
(1)证明:连结AC1交A1C于点F,则F为AC1中点.又D是AB中点,连结DF,则BC1∥DF
|
(2)解:∵ABC-A1B1C1是直三棱柱∴AA1⊥CD
∵AC=CB,D为AB中点,
∴CD⊥AB,
∵AA1∩AB=A,
∴CD⊥平面ABB1A1,
∴AA1=AC=CB=1,AB=
| 2 |
∴∠ACB=90°,CD=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴A1D2+DE2=A1E2,∴DE⊥A1D,
∴VD-A1CE=VC-A1DE=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 8 |
点评:本题主要考查直线和平面平行的判定定理的应用,求三棱锥的体积,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 在直三棱柱ABC-A′B′C′中,底面是以角∠ABC为直角的等腰直角三角形,AC=2a,BB′=3a,D是A′C′的中点.
在直三棱柱ABC-A′B′C′中,底面是以角∠ABC为直角的等腰直角三角形,AC=2a,BB′=3a,D是A′C′的中点. 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形,M、N分别为SB、SD的中点.求证:
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形,M、N分别为SB、SD的中点.求证: 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为 如图是一个组合体的三视图(单位:cm),
如图是一个组合体的三视图(单位:cm),