题目内容
10.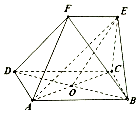 如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF
如图ABCD为矩形,CDFE为梯形,CE⊥平面ABCD,O为BD的中点,AB=2EF(Ⅰ)求证:OE∥平面ADF;
(Ⅱ)若ABCD为正方形,求证:平面ACE⊥平面BDF.
分析 (Ⅰ)如图,取AD的中点M,连接MF,OM.欲证明OE∥平面ADF,只需推知OE∥MF即可;
(Ⅱ)根据平面与平面垂直的判定定理进行证明即可.
解答 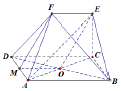 证明:(Ⅰ)如图,取AD的中点M,连接MF,OM,
证明:(Ⅰ)如图,取AD的中点M,连接MF,OM,
因为ABCD为矩形,O为BD的中点,
所以OM∥AB,AB=2OM.
又因为CE⊥平面ABCD,
所以CE⊥CD.因为CDEF为梯形,
所以CD∥EF,
又因为AB=2EF,
所以EF∥OM,EF=OM,
所以EFMO为平行四边形,
所以OE∥MF,
又MF?ADF,所以OE∥平面ADF.
(Ⅱ)因为ABCD为正方形,O为BD的中点,
所以BD⊥AC,
又因为CE⊥平面ABCD,
所以BD⊥CE,
所以BD⊥平面ACE,
所以平面BDF⊥平面ACE.
点评 此题考查立体几何中直线与平面的位置关系,面面垂直问题,考查了空间想象能力.

练习册系列答案
相关题目
20.数列{an}的前项和为${S_n}({n∈{N^*}})$,且${a_1}=\frac{1}{2},{S_n}={n^2}{a_n}({n∈{N^*}})$,利用归纳推理,猜想{an}的通项公式为( )
| A. | ${a_n}=\frac{2n-4}{3^n}$ | B. | ${a_n}=\frac{1}{{n({n+1})}}({n∈{N^*}})$ | C. | ${a_n}=\frac{1}{2n}$ | D. | ${a_n}=\frac{2}{n}$ |
18.阅读下面的程序框图,运行相应的程序,输出的结果为( )


| A. | -3 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
5.某算法的程序框图如图所示,若输出的y=$\frac{{\sqrt{2}}}{2}$,则输入的x的值可能为( )


| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
15.函数f(x)=$\left\{\begin{array}{l}{f(x+3),x<3}\\{lo{g}_{2}(x-1),x≥3}\end{array}\right.$,则f(-1)的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.对于R上可导的任意函数f(x),若满足(x-1)f′(x)≤0,则必有( )
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
20.函数f(x)=ln(-x2+2x+3)的定义域为( )
| A. | {x|-3<x<1} | B. | {x|-1<x<3}. | C. | {x|x<-3或x>1} | D. | {x|x<-1或x>3} |
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )