题目内容
随机变量ξ的分布列如下:
其中a,b,c成等差数列,则函数f(x)=x2+2x+ξ有且只有一个零点的概率为( )
| ξ | 0 | 1 | 2 |
| P | a | b | c |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:离散型随机变量及其分布列,古典概型及其概率计算公式
专题:概率与统计
分析:由已知条件推导出
,由f(x)=x2+2x+ξ有且只有一个零点,得△=4-4ξ=0,由此能求出结果.
|
解答:
解:由题意知
,解得b=
∵f(x)=x2+2x+ξ有且只有一个零点,
∴△=4-4ξ=0,解得ξ=1,
∴P(ξ=1)=
.
故选:B.
|
| 1 |
| 3 |
∵f(x)=x2+2x+ξ有且只有一个零点,
∴△=4-4ξ=0,解得ξ=1,
∴P(ξ=1)=
| 1 |
| 3 |
故选:B.
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等差数列的性质的灵活运用.

练习册系列答案
相关题目
复数z=i(-3-2i)(i为虚数单位)在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )
如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )| A、45° | B、40° |
| C、35° | D、30° |
在一个三角形的三边长之比为3:5:7,则其最大的角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)在x0处可导,
的值为( )
| lim |
| x→x0 |
| f(x0)-f(x) |
| x-x0 |
| A、f′(x0) |
| B、-f′(x0) |
| C、f′(x) |
| D、-f′(x) |
已知x,y∈R,若lne-1i+2=y+xi,则x3+y=( )
| A、9 | B、3 | C、1 | D、2 |
 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=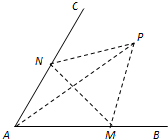 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.