题目内容
6.已知α∈($\frac{3}{2}$π,2π),且满足cos(α+$\frac{2017}{2}$π)=$\frac{3}{5}$,则sinα+cosα=( )| A. | -$\frac{7}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{5}$ |
分析 根据诱导公式化简和同角三角函数关系式,求出sinα,cosα的值.即可求sinα+cosα的值.
解答 解:由cos(α+$\frac{2017}{2}$π)=$\frac{3}{5}$,
可得:cos(1008π+α+$\frac{π}{2}$)=cos($α+\frac{π}{2}$)=-sinα=$\frac{3}{5}$,即sinα=$-\frac{3}{5}$.
∵α∈($\frac{3}{2}$π,2π),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{4}{5}$.
则sinα+cosα=$-\frac{3}{5}+\frac{4}{5}=\frac{1}{5}$.
故选:C.
点评 本题考查了诱导公式化简能力和同角三角函数关系式计算,属于基础题.

练习册系列答案
相关题目
14.设$\overline z=1+i$(i是虚数单位),则在复平面内,${z^2}+\frac{2}{z}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.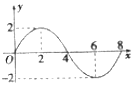 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
15.某体育彩票规定:从01到36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后再从01到17个号中选出3个连续的号,从19到29个号中选出2个连续的号,从30到36个号中选出1个号组成一注.若这个人要把这种要求的号全买,至少要花的钱数为( )
| A. | 2000元 | B. | 3200元 | C. | 1800元 | D. | 2100元 |
16.已知m,n,l是三条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m?α,n?α,n⊥l,则l⊥α | ||
| C. | 若m∥α,n⊥β,α⊥β,则m∥n | D. | 若l⊥α,l⊥β,则α∥β |