题目内容
已知函数f(x)=2sin(ωx),其中常数ω>0.
(1)令ω=
,求函数F(x)=f(x)+f(x+π)的单调区间;
(2)令ω=2,将函数y=f(x)的图象向左平移
个单位,再往上平移1个单位,得到函数y=g(x)的图象.对任意的a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
(1)令ω=
| 1 |
| 2 |
(2)令ω=2,将函数y=f(x)的图象向左平移
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:(1)当ω=
时,利用诱导公式和和差角公式,可将(x)的解析式化为:F(x)=2
sin(
+
),进而结合正弦函数的单调性,可得答案;
(2)ω=2时,f(x)=2sin2x,利用函数图象变化法则,求出函数y=g(x)的解析式,再由正弦函数的图象和性质,可得y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| π |
| 4 |
(2)ω=2时,f(x)=2sin2x,利用函数图象变化法则,求出函数y=g(x)的解析式,再由正弦函数的图象和性质,可得y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
解答:
解:(1)∵f(x)=2sin(ωx),当ω=
时,
由-
+2kπ≤
+
≤
+2kπ,k∈Z得:
x∈[-
+4kπ,
+4kπ],(k∈Z),
即得f(x)的递增单调区间为:[-
+4kπ,
+4kπ],(k∈Z),
由
+2kπ≤
+
≤
+2kπ,k∈Z得:
x∈[
+4kπ,
+4kπ](k∈Z),
即得f(x)的递减单调区间为:[
+4kπ,
+4kπ](k∈Z),
(2)当ω=2时,f(x)=2sin2x,
将函数y=f(x)的图象向左平移
个单位,再往上平移1个单位,
可得y=g(x)=2sin2(x+
)+1=2sin(2x+
)+1的图象,
∵ω=2,
∴函数g(x)的最小正周期T=π,
由2sin(2x+
)+1=0,得sin(2x+
)=-
,
∴2x+
=kπ-(-1)k•
,k∈Z,
即x=
-(-1)k•
-
,k∈Z,
区间[a,a+10π]的长度为10个周期,
若零点不在区间的端点,则每个周期有2个零点;
若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点;
故当a=
-(-1)k•
-
,k∈Z时,21个,否则20个.
| 1 |
| 2 |
|
由-
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
x∈[-
| 3π |
| 2 |
| π |
| 2 |
即得f(x)的递增单调区间为:[-
| 3π |
| 2 |
| π |
| 2 |
由
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
x∈[
| π |
| 2 |
| 5π |
| 2 |
即得f(x)的递减单调区间为:[
| π |
| 2 |
| 5π |
| 2 |
(2)当ω=2时,f(x)=2sin2x,
将函数y=f(x)的图象向左平移
| π |
| 6 |
可得y=g(x)=2sin2(x+
| π |
| 6 |
| π |
| 3 |
∵ω=2,
∴函数g(x)的最小正周期T=π,
由2sin(2x+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴2x+
| π |
| 3 |
| π |
| 6 |
即x=
| kπ |
| 2 |
| π |
| 12 |
| π |
| 6 |
区间[a,a+10π]的长度为10个周期,
若零点不在区间的端点,则每个周期有2个零点;
若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点;
故当a=
| kπ |
| 2 |
| π |
| 12 |
| π |
| 6 |
点评:本题考查的知识点是两角差的正弦函数公式,正弦型函数的单调性,周期性,函数的零点,是三角函数图象和性质的综合应用,难度较大.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
如图,在正方体ABCD-A1B1C1D1中,下列结论不正确的是( )


| A、C1D1⊥B1C |
| B、BD1⊥AC |
| C、BD1∥B1C |
| D、∠ACB1=60° |
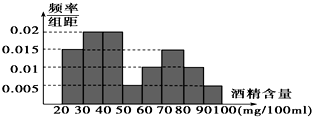 据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.
据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.