题目内容
12.已知直线l1:4x-3y+16=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1的距离为d1,动点P到直线l2的距离为d2,则d1+d2的最小值为4.分析 抛物线y2=4x的焦点F(1,0),由抛物线的定义可得:|PF|=d2,可得d1+d2的最小值为点F到直线l1的距离.
解答 解:抛物线y2=4x的焦点F(1,0),
由抛物线的定义可得:|PF|=d2,
∴d1+d2的最小值为点F到直线l1的距离.
∴d1+d2的最小值=$\frac{|4-0+16|}{5}$=4,
故答案为:4.
点评 本题考查了抛物线的定义及其性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知函数f(x)在其定义域(-∞,0)上是减函数,且f(1-m)<f(m-3),则实数m的取值范围是( )
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
4.已知$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则常数m=( )
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
1.与函数y=$\frac{1}{\sqrt{x-1}}$的定义域相同的函数是( )
| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
2.某同学在求函数y=lgx和$y=\frac{1}{x}$的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
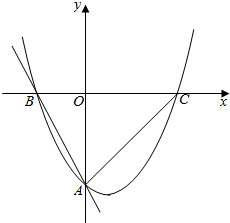 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点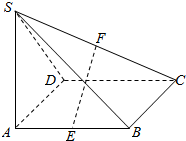 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.