题目内容
根据下列4个图形及黑方块的个数的变化规律，现用f（n）表示第n个图黑方块总数，则f（5）= ，试猜测f（n=） ．
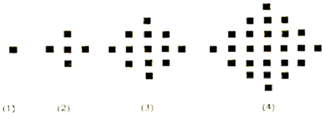
考点：归纳推理
专题：规律型
分析：先分别观察给出正方体的个数为：1，1+4，1+4+8，…总结一般性的规律，将一般性的数列转化为特殊的数列再求解．
解答：
解：根据前面四个发现规律：
f（2）-f（1）=4×1，
f（3）-f（2）=4×2，
f（4）-f（3）=4×3，
…
f（n）-f（n-1）=4（n-1）；
这n-1个式子相加可得：
f（n）=2n2-2n+1．
当n=5时，f（5）=41．
故答案为：（Ⅰ）41；（Ⅱ）2n2-2n+1
f（2）-f（1）=4×1，
f（3）-f（2）=4×2，
f（4）-f（3）=4×3，
…
f（n）-f（n-1）=4（n-1）；
这n-1个式子相加可得：
f（n）=2n2-2n+1．
当n=5时，f（5）=41．
故答案为：（Ⅰ）41；（Ⅱ）2n2-2n+1
点评：本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
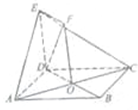如图，O为正方形ABCD的中心，四边形ODEF是平行四边形，且平面ODEF⊥平面ABCD，AD=2，DE=