题目内容
12.在△ABC中,|$\overrightarrow{AB}$|=6,|$\overrightarrow{AC}$|=2|$\overrightarrow{BC}$|,则△ABC的面积的最大值是12.分析 建立坐标系,求出C的轨迹方程,即可求得三角形面积的最大值.
解答 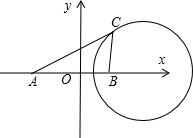 解:建立如图所示的坐标系,则A(-3,0),B(3,0)
解:建立如图所示的坐标系,则A(-3,0),B(3,0)
设C(x,y),
∵|$\overrightarrow{AC}$|=2|$\overrightarrow{BC}$|,∴$\frac{\sqrt{(x+3)^{2}+{y}^{2}}}{\sqrt{(x-3)^{2}+{y}^{2}}}$=2,
化简可得(x-5)2+y2=16,
即C的轨迹是一(5,0)为圆心,4为半径的圆,
∴三角形ABC的面积的最大值为$\frac{1}{2}×6×4$=12.
故答案为:12.
点评 本题考查三角形面积的计算,考查轨迹方程,属于中档题.

练习册系列答案
相关题目
20.下列区间是函数y=2|sinx|的单调递增区间的是( )
| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
7.如某校高中三年级的300名学生已经编号为0,1,…,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.若函数f(x)=x2+3x+2,且f(a)>f(b)>0,则函数f(x)在区间(a,b)内( )
| A. | 一定无零点 | B. | 一定有零点 | C. | 可能有两个零点 | D. | 至多有一个零点 |
2.下列变量是线性相关的是( )
| A. | 人的身高与视力 | B. | 角的大小与弧长 | ||
| C. | 收入水平与消费水平 | D. | 人的年龄与身高 |