题目内容
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$,则目标函数z=|x+3y|的最大值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 先根据约束条件画出可行域,再利用几何意义求最值,只需求出直线z=|x+3y|过点A时,z最大值即可.
解答 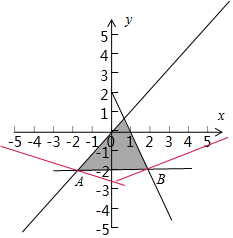 解:作出约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$的可行域如图,
解:作出约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$的可行域如图,
由z=|x+3y|知,所以动折线z=|x+3y|经过可行域A或B点时,z取得最大值时,
目标函数取得最大值.
由$\left\{\begin{array}{l}{y=-2}\\{y=x}\end{array}\right.$得A(-2,-2).由$\left\{\begin{array}{l}{y=-2}\\{2x+y-2=0}\end{array}\right.$解得B(2,-2),
代入目标函数可得zA=8,zB=4
目标函数取得最大值:8.
故选:C.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的体积为( )
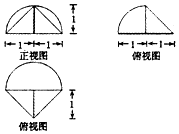

| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△