题目内容
17.执行如图所示的程序框图,若输出的S值为$\frac{1}{3}$,则①处应填写( )
| A. | k<3 | B. | k<4 | C. | k<5 | D. | k<6 |
分析 模拟程序运行过程知S=S+$\frac{1}{{k}^{2}+k}$=S+$\frac{1}{k(k+1)}$=S+$\frac{1}{k}$-$\frac{1}{k+1}$;
计算S=$\frac{1}{3}$时对应的k值,即可得出条件①是什么.
解答 解:模拟程序运行过程,知
S=S+$\frac{1}{{k}^{2}+k}$=S+$\frac{1}{k(k+1)}$=S+$\frac{1}{k}$-$\frac{1}{k+1}$;
k=2时,S=$\frac{1}{2}$-$\frac{1}{3}$≠$\frac{1}{3}$,
k=3时,S=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{2}$-$\frac{1}{4}$≠$\frac{1}{3}$,
k=4时,S=$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$=$\frac{1}{2}$-$\frac{1}{5}$≠$\frac{1}{3}$,
k=5时,S=$\frac{1}{2}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$=$\frac{1}{3}$,此时不满足条件①,输出S=$\frac{1}{3}$;
∴①处为“k<5”.
故选:C.
点评 本题考查了程序框图的应用问题,是基础题.

练习册系列答案
相关题目
5.某校高三毕业汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,要求A、B两个节目要相邻,且都不排在第4号位置,则节目单上不同的排序方式有( )
| A. | 192种 | B. | 144种 | C. | 96种 | D. | 72种 |
12.sin75°sin15°+cos70°cos15°的值为( )
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.从某校随机抽取部分男生进行身体素质测试,获得掷实心球的成绩数据,整理得到数据分组及频率分布表,成绩在11.0米(精确到0.1米)以上(含)的男生为“优秀生”.
(Ⅰ)求参加测试的男生中“优秀生”的人数;
(Ⅱ)从参加测试男生的成绩中,根据表中分组情况,按分层抽样的方法抽取10名男生的成绩作为一个样本,再从该样本中任选2名男生的成绩,求至少选出1名男生的成绩不低于13.0米的概率;
(Ⅲ)若将这次测试的频率作为概率,从该校全体男生中随机抽取3人,记X表示3人中“优秀生”的人数,求X的分布列及数学期望.
| 分组(米) | 频数 | 频率 |
| [3.0,5.0) | 0.10 | |
| [5.0,7.0) | 0.10 | |
| [7.0,9.0) | 0.10 | |
| [9.0,11.0) | 0.20 | |
| [11.0,13.0) | 0.40 | |
| [13.0,15.0) | 10 | |
| 合计 | 1.00 |
(Ⅱ)从参加测试男生的成绩中,根据表中分组情况,按分层抽样的方法抽取10名男生的成绩作为一个样本,再从该样本中任选2名男生的成绩,求至少选出1名男生的成绩不低于13.0米的概率;
(Ⅲ)若将这次测试的频率作为概率,从该校全体男生中随机抽取3人,记X表示3人中“优秀生”的人数,求X的分布列及数学期望.
3.已知定义在R上的函数f(x)满足f($\sqrt{3}$)=-2,f′(x)>-$\sqrt{3}$,若x∈(0,π),则不等式f(2sinx)≤-4$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$+1的解集( )
| A. | [$\frac{π}{3}$,$\frac{2π}{3}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{2π}{3}$,π) | D. | (0,$\frac{π}{3}$]∪[$\frac{2π}{3}$,π) |
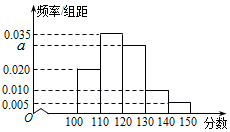 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.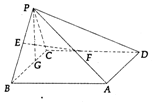 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$