题目内容
9.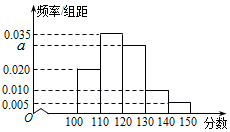 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
分析 由频率分布直方图中小矩形有面积之和为1,能求出a;由频率分布直方图得:成绩在[120,130)内的学生有60人,成绩在[130,140)内的学生有20人,成绩在[140,150]内的学生有10人,要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,能求出从成绩在[130,140)内的学生中选取的人数.
解答 解:由频率分布直方图,得:
0.020+0.035+a+0.010+0.005=$\frac{1}{10}$,
解得a=0.030.
由频率分布直方图得:成绩在[120,130)内的学生有:200×0.030×10=60人,
成绩在[130,140)内的学生有:200×0.010×10=20人,
成绩在[140,150]内的学生有:200×0.005×10=10人,
要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,
则从成绩在[130,140)内的学生中选取的人数应为:18×$\frac{20}{60+20+10}$=4.
故答案为:0.030,4.
点评 本题考查概率的求法,考查频数的求法,考查频率分布直方图、分层抽样等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
19.函数f(x)=ln(x+1)-$\frac{2}{{x}^{2}}$的零点所在的大致区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
20.在半径为2的圆中,1弧度的圆心角所对应的扇形的面积是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.执行如图所示的程序框图,若输出的S值为$\frac{1}{3}$,则①处应填写( )


| A. | k<3 | B. | k<4 | C. | k<5 | D. | k<6 |
4.已知$\overrightarrow{a}$=(1,$\sqrt{3}$),b=($\sqrt{3}$,k),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
14.不等式组$\left\{\begin{array}{l}x+y-\sqrt{2}≤0\\ x-y+\sqrt{2}≥0\\ y≥0\end{array}\right.$所围成的平面区域的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.过点(-10,10)且在x轴上截距是在y轴上截距的4倍的直线的方程为( )
| A. | x-y=0 | B. | x+4y-30=0 | ||
| C. | x+y=0 或x+4y-30=0 | D. | x+y=0或x-4y-30=0 |
16.若关于x的方程|f(|x|)|=a,当a>0时总有4个解,则f(x)可以是( )
| A. | x2-1 | B. | $\frac{1}{x-1}$ | C. | 2x-2 | D. | log2x-2 |
