题目内容
4.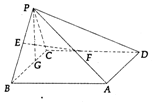 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$(1)点E,F分别为线段BP,DC中点,求证:EF∥平面APD
(2)设G为线段BC上的一点,且BG=2GC,求证:PG⊥平面ABCD.
分析 (1)取PA中点M,连接EM,MD,推导出EFDM为平行四边形,从而EF∥MD,由此能证明EF∥平面APD.
(2)取PC中点N,连接NB,过P点作PG'⊥BC,垂足为G',推导出PG⊥BC,AB⊥BC,AB⊥PC,从而AB⊥平面PBC,进而平面PBC⊥平面ABCD,PG⊥BC,由此能证明PG⊥平面ABCD.
解答 证明:(1)取PA中点M,连接EM,MD,
在△PBA中,E,M分别为PB,PA的中点,∴$EM\underline{\underline{∥}}\frac{1}{2}BA$,
在矩形ABCD中,F为DC中点,∴$FD\underline{\underline{∥}}\frac{1}{2}BA$,
∴$EM\underline{\underline{∥}}FD$,∴EFDM为平行四边形,
∴EF∥MD,又EF?平面APD,MD?平面APD,
∴EF∥平面APD.
(2)取PC中点N,连接NB,由$BP=BC=3,PC=\sqrt{6}$,∴$BN=\frac{{\sqrt{30}}}{2}$,
过P点作PG'⊥BC,垂足为G',则$PG'=\frac{BN•PC}{BC}=\sqrt{5}$,
∴$BG'=\sqrt{P{B^2}-P{{G'}^2}}=2$,由G为线段BC上一点,BG=2,
可知G,G'重合.即PG⊥BC,
∵AB⊥BC,AB⊥PC,BC∩PC=C,BC?平面PBC,PC?平面PBC,
∴AB⊥平面PBC,AB?平面ABCD,∴平面PBC⊥平面ABCD,
∵平面PBC∩平面ABCD=BC,且PG⊥BC,
∴PG⊥平面ABCD.
点评 本题考查线面平行、线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


| A. | k<3 | B. | k<4 | C. | k<5 | D. | k<6 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | x2-1 | B. | $\frac{1}{x-1}$ | C. | 2x-2 | D. | log2x-2 |
| A. | (-∞,2] | B. | (-∞,$\frac{5}{2}$] | C. | [2,$\frac{5}{2}$] | D. | [$\frac{5}{2}$,+∞) |
