题目内容
用适当的符号填空:
(1)0 {x|x2=0},
(2)∅ {x∈R|x2+1=0},
(3){0,1} N.
(1)0
(2)∅
(3){0,1}
考点:集合的包含关系判断及应用,元素与集合关系的判断
专题:计算题,集合
分析:选确定空格前后分别是集合还是元素,而后判断关系.
解答:
解:(1){x|x2=0}={0},故0∈{x|x2=0},
(2)∵x2+1=0无解,∴{x∈R|x2+1=0}=Φ,
(3){0,1}⊆N.
故答案为:(1)∈;(2)=;(3)⊆.
(2)∵x2+1=0无解,∴{x∈R|x2+1=0}=Φ,
(3){0,1}⊆N.
故答案为:(1)∈;(2)=;(3)⊆.
点评:本题考查了元素与集合,集合与集合之间的关系,注意正确选择符号.

练习册系列答案
相关题目
设f(x+2)=2x+1,则f(2)等于( )
| A、1 | B、2 | C、3 | D、4 |
 若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )
若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )| A、30 | B、12 | C、24 | D、4 |
下列函数中,既是奇函数又在[-1,1]上是单调递减的函数是( )
| A、f(x)=sinx | ||
| B、f(x)=-|x-1| | ||
C、f(x)=
| ||
D、f(x)=ln
|
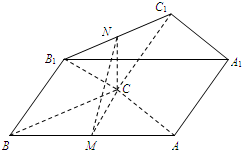 如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点. 如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2