题目内容
(2x-1)4(2x+1)6的展开式中含x4的系数为( )
| A、-32 | B、32 |
| C、-92 | D、100 |
考点:二项式系数的性质
专题:二项式定理
分析:将问题转化成(4x2-1)4(2x+1)2展开式中含x4的系数,利用二项展开式的通项公式求出.
解答:
解:(2x-1)4(2x+1)6=(4x2-1)4(2x+1)2展开式中含x4项的系数:
是两个因式的展开式中含x2的系数乘积,以及第一个因式x4项的系数与第二个因式的常数项的乘积.
(4x2-1)4展开式中含x2的项是C43(4x2)(-1)3=-16x2
(4x2-1)4展开式中含x4的项是C42(4x2)2(-1)2=96.
故展开式中含x4项的系数为:-16×4+96=32.
故选:B.
是两个因式的展开式中含x2的系数乘积,以及第一个因式x4项的系数与第二个因式的常数项的乘积.
(4x2-1)4展开式中含x2的项是C43(4x2)(-1)3=-16x2
(4x2-1)4展开式中含x4的项是C42(4x2)2(-1)2=96.
故展开式中含x4项的系数为:-16×4+96=32.
故选:B.
点评:本题考查数学的等价转化能力,考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图所示的三视图的几何体的体积为( )


A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
如果椭圆
+
=1上一点p到焦点F1的距离等于3,那么点p到另一个焦点F2的距离是( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、4 | B、3 | C、2 | D、1 |
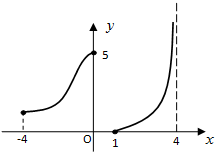 如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )
如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )| A、函数f(x)的定义域为[-4,4) |
| B、函数f(x)的值域为[0,5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
点P分有向线段
的比为λ(即
=λ
),且|
|=3|
|,则λ的值是( )
| MN |
| MP |
| PN |
| MN |
| NP |
| A、4或-2 | B、-3或1 |
| C、-4或2 | D、-3或-1 |
在△ABC中,A,B,C所对的边分别是a,b,c,满足3a2+3b2=c2+4ab,现设f(x)=tanx,则( )
| A、f(sinA)≤f(cosB) |
| B、f(sinA)≥f(cosB) |
| C、f(sinA)≤f(sinB) |
| D、f(cosA)≤f(cosB) |
双曲线
-
=1的渐近线方程是( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、2x±3y=0 |
| B、3x±2y=0 |
| C、9x±4y=0 |
| D、4x±9y=0 |