题目内容
在半径为2的圆内随机地取一点A,以点A为中点做一条弦PQ,求弦PQ长超过圆内接正三角形的边长概率是多少( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意可得:符合条件的点必须在内接等边三角形的内切圆内,所求概率为两圆的面积比,利用几何概型的概率公式即可得到结论.
解答:
解:由题意可得:当点A为中点做一条弦PQ,
若弦PQ长超过圆内接正三角形的边长BC,则点A必须位于△BCD的内切圆内,
因为两圆的圆心相同,大圆的半径为2,故内接正三角形的边长为2
,故内接等边三角形的内切圆半径OD=1,
由几何概型的概率公式可知弦PQ长超过圆内接正三角形的边长概率P=
=
=
故选:C

若弦PQ长超过圆内接正三角形的边长BC,则点A必须位于△BCD的内切圆内,
因为两圆的圆心相同,大圆的半径为2,故内接正三角形的边长为2
| 3 |
由几何概型的概率公式可知弦PQ长超过圆内接正三角形的边长概率P=
| S小圆 |
| S大圆 |
| π×12 |
| π×22 |
| 1 |
| 4 |
故选:C
点评:本题主要考查几何概型的计算,根据题意确定A满足的条件是解决本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
设(2+i)
=3+4i,则z=( )
. |
| z |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
已知等比数列{an}中,a2+a3=1,a4+a5=2,则a6+a7等于( )
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
已知向量
=(1,x),
=(x-1,2),若
∥
,则x=( )
| a |
| b |
| a |
| b |
| A、-1或2 | B、-2或1 |
| C、1或2 | D、-1或-2 |
球面上有M、N两点,在过M、N的球的大圆上,
的度数为90°,在过M、N的球小圆上,
的度数为120°,又MN=
cm,则球心到上述球小圆的距离是( )
 |
| MN |
 |
| MN |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
设点P(x,y),其中x,y∈N,则满足x+y≤3的点P的个数为( )
| A、10 | B、9 | C、3 | D、无数 |
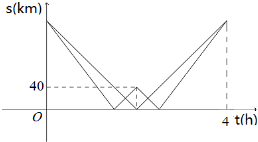 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行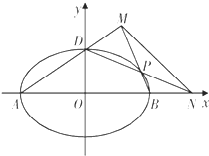 已知椭圆
已知椭圆