题目内容
9．已知点的极坐标为$（2，\frac{2π}{3}）$那么它的直角坐标为（ ）| A． | $（\sqrt{3}，-1）$ | B． | $（-\sqrt{3}，-1）$ | C． | $（-1，\sqrt{3}）$ | D． | $（-1，-\sqrt{3}）$ |
分析 利用x=ρcosθ，y=ρsinθ即可得出直角标准．
解答 解：点的极坐标为$（2，\frac{2π}{3}）$，可得它的直角坐标x=2$cos\frac{2π}{3}$=-1，y=2$sin\frac{2π}{3}$=$\sqrt{3}$．即$（-1，\sqrt{3}）$．
故选：C．
点评 本题考查了极坐标化为直角坐标，考查了推理能力与计算能力，属于基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
10．已知复数z满足（2+i）z=2-i（i为虚数单位），则z=（ ）
| A． | 3+4i | B． | 3-4i | C． | $\frac{3}{5}$+$\frac{4}{5}$i | D． | $\frac{3}{5}$-$\frac{4}{5}$i |
4．某地区2007年至2013年农村居民家庭人均纯收入y（单位：千元）的数据如表：
y关于t的线性回归方程为$\stackrel{∧}{y}$=0.5t+2.3，则a的值为4.8．
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
14．为了研究某种微生物的生长规律，需要了解环境温度x（°C）对该微生物的活性指标y的影响，某实验小组设计了一组实验，并得到如表的实验数据：
（Ⅰ）由表中数据判断y关于x的关系较符合$\widehaty=\widehatbx+\widehata$还是$\widehaty={2^{\widehatbx+\widehata}}$，并求y关于x的回归方程（$\widehata$，$\widehatb$取整数）；
（Ⅱ）根据（Ⅰ）中的结果分析：若要求该种微生物的活性指标不能低于26.3，则环境温度应不得高于多少°C？
附：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
| 环境温度x（°C） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 活性指标y | 28 | 27 | 26 | 24 | 25 | 23 | 22 |
（Ⅱ）根据（Ⅰ）中的结果分析：若要求该种微生物的活性指标不能低于26.3，则环境温度应不得高于多少°C？
附：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
1．一个空间几何体的三视图及部分数据如下图所示，则该几何体的体积是（ ）
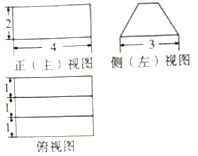
| A． | $\frac{{32+8\sqrt{3}}}{3}$ | B． | 16 | C． | 12 | D． | $32+8\sqrt{3}$ |
18．曲线C1：ρsinθ-2=0，曲线C2：ρ-4cosθ=0，则曲线C1、C2的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 重合 | D． | 相离 |