题目内容
设数列{an}为等差数列,其公差为d,数列{bn}为等比数列,若a1<a2,b1<b2,且b1=ai2(i=1,2,3),则
.
| a1 |
| d |
考点:等差数列的性质
专题:等差数列与等比数列
分析:设等差数列{an}的公差为d,可得d>0,由数列{bn}为等比数列,可得b22=b1•b3,代入化简可得a1和d的关系,分类讨论可得b1和b2,可得结论.
解答:
解:设等差数列{an}的公差为d,
由a1<a2可得d>0,
∴b1=a12,b2=a22=(a1+d)2,b3=a32=(a1+2d)2,
∵数列{bn}为等比数列,
∴b22=b1•b3,
即(a1+d)4=a12•(a1+2d)2,
∴(a1+d)2=a1•(a1+2d) ①
或(a1+d)2=-a1•(a1+2d),②
由①可得d=0与d>0矛盾,应舍去;
由②可得a1=
d,或a1=
-1d,
当a1=
d时,可得b1=a12=
d2
b2=a22=(a1+d)2=
d2,此时显然与b1<b2矛盾,舍去;
当a1=
-1d时,可得b1=a12=
d2,b2=(a1+d)2=
d2,满足题意,
∴
=
-1,
故答案为:
-1.
由a1<a2可得d>0,
∴b1=a12,b2=a22=(a1+d)2,b3=a32=(a1+2d)2,
∵数列{bn}为等比数列,
∴b22=b1•b3,
即(a1+d)4=a12•(a1+2d)2,
∴(a1+d)2=a1•(a1+2d) ①
或(a1+d)2=-a1•(a1+2d),②
由①可得d=0与d>0矛盾,应舍去;
由②可得a1=
-2-
| ||
| 2 |
| ||
| 2 |
当a1=
-2-
| ||
| 2 |
3+2
| ||
| 2 |
b2=a22=(a1+d)2=
| 1 |
| 2 |
当a1=
| ||
| 2 |
3-2
| ||
| 2 |
| 1 |
| 2 |
∴
| a1 |
| d |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查等差数列与等比数列的性质,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
已知i是虚数单位,则
=( )
| i |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
“x≠1且y≠2”是“x+y≠3”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
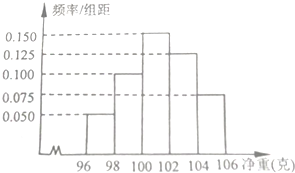 某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是
某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是 如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.