题目内容
20．已知集合A={0，1}，B={x|x2-ax=0}，且A∪B=A，求实数a的值．分析 先求出集合B中的元素，根据并集的运算，求出a的值即可．
解答 解：∵B={x|x2-ax=0}，∴B={x|x=0或x=a}，
由A∪B=A，得B={0}或{0，1}．（4分）
当B={0}时，方程x2-ax=0有两个相等实数根0，∴a=0．（6分）
当B={0，1}时，方程x2-ax=0有两个实数根0，1，∴a=1．（8分）
点评 本题考查了集合的并集的定义，考查分类讨论思想，是一道基础题．
练习册系列答案
相关题目
11．假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：
由资料可知y对x呈线性相关关系，且线性回归方程为$\hat y=1.2x+a$，请估计使用年限为20年时，维修费用约为（ ）
| x | 1 | 2 | 3 | 4 | 5 |
| y | 5 | 6 | 7 | 8 | 10 |
| A． | 26.2 | B． | 27 | C． | 27.6 | D． | 28.2 |
15．如果过点M（-2，0）的直线l与椭圆$\frac{x^2}{2}+{y^2}=1$有公共点，那么直线l的斜率k的取值范围是（ ）
| A． | $（-∞，-\frac{{\sqrt{2}}}{2}]$ | B． | $[\frac{{\sqrt{2}}}{2}，+∞）$ | C． | $[-\frac{1}{2}，\frac{1}{2}]$ | D． | $[-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}]$ |
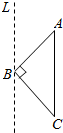如图，等腰直角三角形ABC，|AB|=$\sqrt{2}$，AC∥L，三角形ABC绕直线L旋转一周，得到的几何体的体积为$\frac{4π}{3}$．
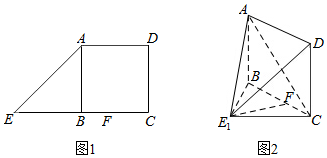如图1，在直角梯形ADCE中，AD∥EC，EC=2BC，∠ADC=90°，AB⊥EC，点F为线段BC上的一点．将△ABE沿AB折到△ABE1的位置，使E1F⊥BC，如图2．