题目内容
定义在{x|x∈R,x≠1}上的函数f(1-x)=-f(1+x),当x>1时,f(x)=(
)x,则函数g(x)=f(x)-
cosπ(x+
)(-3≤x≤5)的所有零点之和等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、10 | B、8 | C、6 | D、4 |
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:根据f(1-x)=-f(1+x),可得函数关于(1,0)对称.构造函数f(x)=(
)x,h(x)=
cosπ(x+
)=-
sinπx(-3≤x≤5),当x>1时,两函数图象的交点共有4个,根据对称性,可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:∵f(1-x)=-f(1+x),
解:∵f(1-x)=-f(1+x),
∴函数关于(1,0)对称.
构造函数f(x)=(
)x,h(x)=
cosπ(x+
)=-
sinπx(-3≤x≤5),
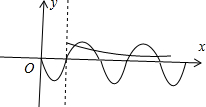
当x>1时,两函数图象的交点共有4个,
∴根据对称性,可得两函数图象的交点共有8个.
故选B.
 解:∵f(1-x)=-f(1+x),
解:∵f(1-x)=-f(1+x),∴函数关于(1,0)对称.
构造函数f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x>1时,两函数图象的交点共有4个,
∴根据对称性,可得两函数图象的交点共有8个.
故选B.
点评:本题考查函数的零点,解题的关键是构造函数,确定函数图象的对称性及图象的交点的个数.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
∫
sin2
dx=( )
0 |
| x |
| 2 |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
下例等式中,对任意实数α,β均满足的是( )
A、tan(α+β)=
| ||
B、tan(α-β)=
| ||
| C、cos2α=2cos2α-1 | ||
| D、sin2α-2sin2α=1 |