题目内容
已知函数f(x)=2sin(2x-
),若x∈[0,
]时函数y=f(x)+a的最小值为-2,求实数a的值.
| π |
| 6 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:当x∈[0,
]时,2x-
∈[-
,
],根据正弦函数的定义域和值域求得函数的最小值,再根据最小值为-2,求得a的值.
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解答:
解:∵函数f(x)=2sin(2x-
),当x∈[0,
]时,2x-
∈[-
,
],
故当2x-
=-
时,函数y=f(x)+a取得最小值为-1+a=-2,
求得 a=-1.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
故当2x-
| π |
| 6 |
| π |
| 6 |
求得 a=-1.
点评:本题主要考查正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)是R上的偶函数,且在[0,+∞)上为增函数,则( )
| A、f(-π)>f(3)>f(-2) |
| B、f(-π)>f(-2)>f(3) |
| C、f(-π)<f(3)<f(-2) |
| D、f(-π)<f(-2)<f(3) |
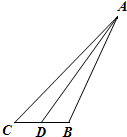 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cos2α=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cos2α=- 如图,扇形所含的中心角是90°,弦AB将扇形分成两个部分,各以AO为轴旋转一周所得的旋转体体积V1 与V2的比是=
如图,扇形所含的中心角是90°,弦AB将扇形分成两个部分,各以AO为轴旋转一周所得的旋转体体积V1 与V2的比是=