题目内容
下例等式中，对任意实数α，β均满足的是（ ）
A、tan（α+β）=
| ||
B、tan（α-β）=
| ||
| C、cos2α=2cos2α-1 | ||
| D、sin2α-2sin2α=1 |
考点：三角函数的化简求值
专题：三角函数的求值
分析：根据两角和差的正切公式以及余弦和正弦的倍角公式即可进行判断．
解答：
解：A．当α=
+kπ，β=
+kπ，时正切公式不成立．
B．当α=
+kπ，β=
+kπ，时正切公式不成立．
C．cos2α=2cos2α-1恒成立．
D．当α=0时，sin2α-2sin2α=1不成立．
故选：C．
| π |
| 2 |
| π |
| 2 |
B．当α=
| π |
| 2 |
| π |
| 2 |
C．cos2α=2cos2α-1恒成立．
D．当α=0时，sin2α-2sin2α=1不成立．
故选：C．
点评：本题主要考查三角函数公式成立的条件，比较基础．
练习册系列答案
相关题目
设函数f（x）是R上的偶函数，且在[0，+∞）上为增函数，则（ ）
| A、f（-π）＞f（3）＞f（-2） |
| B、f（-π）＞f（-2）＞f（3） |
| C、f（-π）＜f（3）＜f（-2） |
| D、f（-π）＜f（-2）＜f（3） |
已知函数f（x）=x2-2ln|x|与g（x）=sin（x+ψ）（ω＞0）有两个公共点，则在下列函数中满足条件的周期最大的g（x）等于（ ）
A、sin（2πx-
| ||||
B、sin（
| ||||
C、sin（πx-
| ||||
D、sin（πx+
|
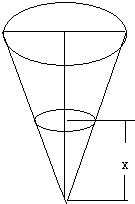如图，圆锥型量杯口径为2R，高为h，求量杯母线上刻度V（容积）与液面深x的函数关系．