题目内容
证明恒等式：
=sec2α+csc2α．
| tan2α-cot2α |
| sin2α-cos2α |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左右两边利用同角三角函数间基本关系化简，即可得证．
解答：
证明：左边=
=
=
=
，
右边=
+
=
=
，
∴左边=右边，
则原等式成立．
| ||||
| sin2α-cos2α |
| sin4α-cos4α |
| sin2αcos2α(sin2α-cos2α) |
| (sin2α+cos2α)(sin2α-cos2α) |
| sin2αcos2α(sin2α-cos2α) |
| 1 |
| sin2αcos2α |
右边=
| 1 |
| cos2α |
| 1 |
| sin2α |
| sin2α+cos2α |
| sin2αcos2α |
| 1 |
| sin2αcos2α |
∴左边=右边，
则原等式成立．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）在x=
处取得最小值，则（ ）
| π |
| 4 |
A、f（x+
| ||
B、f（x+
| ||
C、f（x-
| ||
D、f（x-
|
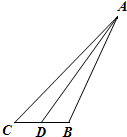如图，在△ABC中，∠C=45°，D为BC中点，BC=2．记锐角∠ADB=α．且满足cos2α=-
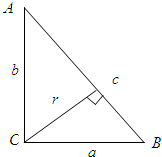设直角△ABC的直角边BC=a，AC=b，斜边AB=c，且a＜b，现分别以直线BC，AC和AB为轴将直角△绕轴旋转一周，所得三个旋转体体积分别为V1，V2和V3，试比较V1，V2，V3的大小．