题目内容

已知△ABC的三条边长分别为8，10，15，则该三角形为（　　）
A、钝角三角形B、直角三角形
C、锐角三角形D、不能确定
考点：余弦定理
专题：解三角形
分析：利用余弦定理得出最大边15所对的角即可判断出．
解答： 解：设边15所对的角为θ，则cosθ=
82+102-152
2×8×10
＜0，
因此角θ为钝角，
∴该三角形为钝角三角形．
故选：A．
点评：本题考查了余弦定理的应用、三角形形状的判定方法，考查了计算能力，属于基础题．
练习册系列答案
相关题目
集合A={x|
x-1
x+1
≥2，x∈Z}的子集个数为（　　）
A、2B、3C、4D、5
在△ABC中，若
AB
=
a
，
AC
=
b‘

（1）若D为BC上的点，且
BD
=t
BC
，求证：
AD
=（1-t）
a
+t
b
；
（2）若P，Q是线段BC的三等分点，试证：
AP
+
AQ
=
a
+
b
；
（3）若P，Q，S是线段BC的四等分点，试证：
AP
+
AQ
+
AS
=
3
2
(
a
+
b
)
（4）如果A1，A2，A3，…An-1是线段BC的n（n≥3）等分点，你能得到什么结论？并加以证明．（注：1+2+3+…+n=
n(n+1)
2
）
某几何体的三视图如图所示，那么该几何体的表面积为（　　）
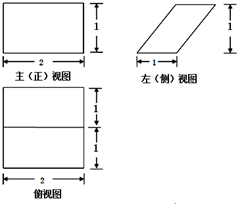
A、2
B、14
C、6+4
2
D、4+6
2
如图，椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右两焦点分别为F1，F2，离心率e=
1
2
．设P（x0，y0）为椭圆上第一象限内的点，△PF1F2的周长为6．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若直线l：3x0x+4y0y-12=0分别与直线x=±2交于C、D两点．
（1）判断直线l与椭圆E交点的个数；
（2）试探究：在坐标平面内是否存在定点，使得以CD为直径的圆恒过该定点？若存在，求出此定点的坐标；若不存在，说明理由．
已知f（x）=2sin（2x+
π
3
）+1
（1）在直角坐标系中用“五点画图法”画出f（x）一个周期的图象（要求列表、描点）
（2）直接写出函数f（x）的单调递增区间以及f（x）取最大值时的所有x值的集合．
9台发动机分别安装在甲、乙、丙3个车间内，每个车间3台，每台发动机正常工作的概率为
1
2
．若一个车间内至少有一台发动机正常工作，则这个车间不需要停产维修，否则需要停产维修．
（1）求甲车间不需要停产维修的概率；
（2）若每个车间维修一次需1万元（每月至多维修一次），用ξ表示每月维修的费用，求ξ的分布列及数学期望．
在棱长都相等的四面体ABCD中，M，N分别为BC，CD的中点，则MN与AC所成角为（　　）
A、30°B、45°
C、60°D、90°
设函数y=x
1
3
与y=（
1
2
）x的图象的交点为（x0，y0），则x0所在的区间是（　　）
A、（
1
2
，1）
B、（
1
3
，
1
2
）
C、（
1
4
，
1
3
）
D、（0，
1
4
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网