题目内容
运行程序框图所对应的程序，输出结果s的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点：程序框图
专题：计算题,算法和程序框图
分析：算法的功能是求S=sin
+sin
+…+sin
的值，根据条件确定跳出循环的n值，利用正弦函数的周期性计算输出S的值．
| π |
| 3 |
| 2π |
| 3 |
| nπ |
| 3 |
解答：
解：由程序框图知：算法的功能是求S=sin
+sin
+…+sin
的值，
∵跳出循环的n值为2015，
又sin
+sin
+sin
+sin
+sin
+sin
=sin
+sin
+sin
-sin
-sin
-sin
=0，
2014=6×365+4，
∴输出S=sin
+sin
+sin
+sin
=
．
故选：B．
| π |
| 3 |
| 2π |
| 3 |
| nπ |
| 3 |
∵跳出循环的n值为2015，
又sin
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
| (n+3)π |
| 3 |
| (n+4)π |
| 3 |
| (n+5)π |
| 3 |
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
2014=6×365+4，
∴输出S=sin
| π |
| 3 |
| 2π |
| 3 |
| 3π |
| 3 |
| 4π |
| 3 |
| ||
| 2 |
故选：B．
点评：本题考查了当型循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键．
练习册系列答案
相关题目
从一篮子鸡蛋中任取1个，如果其重量小于30克的概率为0.3，重量在[30，40]克的概率为0.5，那么重量不小于30克的概率为（ ）
| A、0.3 | B、0.5 |
| C、0.8 | D、0.7 |
已知sinα+sinβ+sinγ=0，cosα+cosβ-cosγ=0，则cos（α-β）的值是（ ）
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
函数y=3sinx+2cosx的最小值是（ ）
| A、0 | ||
| B、-3 | ||
| C、-5 | ||
D、-
|
函数f（x）=（x2-2）（x2-3x+2）的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
设M是椭圆
+
=1上的一点，F1、F2为焦点，∠F1MF2=
，则S△ MF1F2为（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| π |
| 3 |
A、
| ||||
B、16
| ||||
C、
| ||||
D、25
|
在Rt△ABC中，A=90°，AB=1，则
•
的值是（ ）
| AB |
| BC |
| A、1 |
| B、-1 |
| C、1或-1 |
| D、不确定，与B的大小，BC的长度有关 |
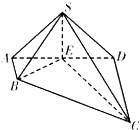如图，四棱锥S-ABCD中，AB⊥AD，AB∥CD，CD=3AB=3，平面SAD⊥平面ABCD，E是线段AD上一点，AE=ED=