Question

经过极坐标为（0，0），（6，

π

2

），（6

2

，

π

4

）三点的圆的极坐标方程为

 

．

Answer 1

考点：简单曲线的极坐标方程

专题：坐标系和参数方程

分析：设（ρ，θ）是所求圆上的任意一点，则由OP=OBcos（θ-

π

4

），求出圆的极坐标方程．

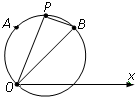
解答： 解：所求的圆经过三点分别为，O，A，B．
不妨记O（0，0），A（6，

π

2

），B（6

2

，

π

4

），设（ρ，θ）是所求圆上的任意一点，…3分
则OP=OBcos（θ-

π

4

），
故所求的圆的极坐标方程为 ρ=6

2

cos（θ-

π

4

）．  …10分

故答案为：ρ=6

2

cos（θ-

π

4

）．

点评：本题主要考查求圆的极坐标方程的方法，点的极坐标的意义，属于基础题．