题目内容
已知点M（-1，1，-2），平面π过原点O，且垂直于向量
=（1，-2，2）．求点M到平面π的距离．
| n |
考点：点、线、面间的距离计算,空间两点间的距离公式
专题：空间位置关系与距离
分析：确定
、
•
，利用点M到平面π的距离为d=
，即可求得结论．
| MO |
| MO |
| n |
| ||||
|
|
解答：
解：由题意，
=（1，-1，2），
=（1，-2，2），
•
=1+2+4=7
设
、
的夹角为α，则
•
=|
||
|cosα
∴点M到平面π的距离为d=|
|cosα=
=
．
点M到平面π的距离：
．
| MO |
| n |
| MO |
| n |
设
| MO |
| n |
| MO |
| n |
| MO |
| n |
∴点M到平面π的距离为d=|
| MO |
| ||||
|
|
| 7 |
| 3 |
点M到平面π的距离：
| 7 |
| 3 |
点评：本题考查空间向量，考查点到面的距离的计算，属于基础题．
练习册系列答案
相关题目
已知数列{an}对任意的n∈N*有an+1=an-
+1成立，若a1=1，则a10等于（ ）
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P为抛物线y2=4x上一动点，则点P到y轴的距离与到点A（2，3）的距离之和的最小值为（ ）
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
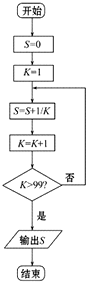给出一个算法的程序框图（如图所示）．
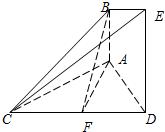如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．