题目内容
18. 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
分析 (Ⅰ)由频率分布直方图求出成绩落在[70,80)上的频率,由此能补全这个频率分布直方图.
(Ⅱ) 利用频率分布直方图能估计这次考试的及格率和平均分.
(Ⅲ) 成绩在[40,50)的学生人数为6人,成绩在[90,100]的学生人数为3人,从成绩在[40,50)和[90,100]的学生中任选两人,基本事件总数n=${C}_{9}^{2}$=36,他们在同一分数段包含的基本事件个数m=${C}_{6}^{2}+{C}_{3}^{2}$=18,由此能求出他们在同一分数段的概率.
解答 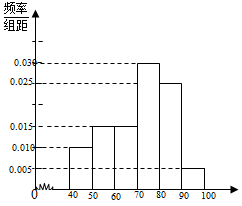 解:(Ⅰ)由频率分布直方图得:
解:(Ⅰ)由频率分布直方图得:
成绩落在[70,80)上的频率是:1-(0.010+0.015+0.015+0.025+0.005)×10=0.3,
补全频率分布直方图如右图.…(4分)
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)为:1-0.01×10-0.015×10=75%
平均分为:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71(分).…(8分)
(Ⅲ) 成绩在[40,50)的学生人数为0.010×10×60=6人,成绩在[90,100]的学生人数为0.005×10×60=3人,
从成绩在[40,50)和[90,100]的学生中任选两人,基本事件总数n=${C}_{9}^{2}$=36,
他们在同一分数段包含的基本事件个数m=${C}_{6}^{2}+{C}_{3}^{2}$=18,
∴他们在同一分数段的概率p=$\frac{m}{n}$=$\frac{18}{36}$=$\frac{1}{2}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.

练习册系列答案
相关题目
9.已知直线ax+y+1=0与x+(a+$\frac{3}{2}$)y+2=0平行,则实数a=( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$或-2 | D. | 2或-$\frac{1}{2}$ |
6.将-$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα化成Asin(α+β)(A>0,0<β<2π)的形式,以下式子正确的是( )
| A. | sin(α+$\frac{4π}{3}$) | B. | sin(α+$\frac{7π}{6}$) | C. | -sin(α+$\frac{π}{3}$) | D. | sin(α-$\frac{2π}{3}$) |
13.函数f(x)=ax-1-2(a>0,a≠1)的图象恒过定点A,若点A在直线mx-ny-1=0上,其中m>0,n>0,则$\frac{1}{m}$+$\frac{2}{n}$的最小值为( )
| A. | 4 | B. | 5 | C. | 7 | D. | 3+2$\sqrt{2}$ |
7.命题“?x∈[1,2],x2-2x-a≤0”为真命题的一个充分不必要条件是( )
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |
 在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,则该35名运动员成绩的中位数为143.
在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,则该35名运动员成绩的中位数为143.