题目内容
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
(1)设等比数列{an}的公比为q,
∵ an+1+an=9·2n-1,n∈N*,∴ a2+a1=9,a3+a2=18,
∴ q= =
= =2,
=2,
∴ 2a1+a1=9,∴ a1=3.
∴ an=3·2n-1,n∈N*.
(2)由(1),知Sn= =3(2n-1),
=3(2n-1),
∴ 不等式3(2n-1)>k·3·2n-1-2,
即k<2- 对一切n∈N*恒成立.
对一切n∈N*恒成立.
令f(n)=2- ,则f(n)随n的增大而增大,
,则f(n)随n的增大而增大,
∴ f(n)min=f(1)=2-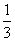 =
= ,∴ k<
,∴ k< .
.
∴ 实数k的取值范围为 .
.

练习册系列答案
相关题目


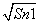 +
+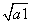 )2(n≥2),若bn=
)2(n≥2),若bn=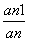 +
+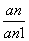 ,且数列{bn}的前n项的和为Tn,则Tn=__________.
,且数列{bn}的前n项的和为Tn,则Tn=__________. 的图象上各点的横坐标伸长到原来的3倍,再向右平移
的图象上各点的横坐标伸长到原来的3倍,再向右平移 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )
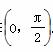 .
.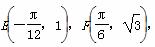 求函数f(x)的解析式;
求函数f(x)的解析式;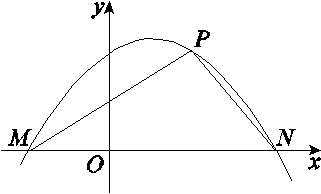
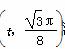 满足
满足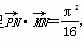 ,求函数f(x)的最大值.
,求函数f(x)的最大值. +i的共轭复数为________.
+i的共轭复数为________.