题目内容
18. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是冷BC的中点,点F在冷CC1上,且CF=2FC1,P是侧面四边形BCC1B1内一点(含边界).若A1P∥平面AEF,则线段
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是冷BC的中点,点F在冷CC1上,且CF=2FC1,P是侧面四边形BCC1B1内一点(含边界).若A1P∥平面AEF,则线段A1P长度的取值范围是( )
| A. | $[{\frac{{\sqrt{29}}}{5},\frac{{\sqrt{5}}}{2}}]$ | B. | $[{\frac{{\sqrt{29}}}{5},\frac{{\sqrt{13}}}{3}}]$ | C. | $[{\frac{{3\sqrt{2}}}{4},\frac{{\sqrt{13}}}{3}}]$ | D. | $[{\frac{{3\sqrt{2}}}{4},\frac{{\sqrt{5}}}{2}}]$ |
分析 取棱B1C1的中点N,在BB1上取点M,使B1M=2BM,连接MN,易证平面A1MN∥平面AEF,由题意知点P必在线段MN上,由此可判断P在M处时A1P最长,A1P⊥MN时最短,通过解直角三角形即可求得.
解答 解:如下图所示:
取棱B1C1的中点N,在BB1上取点M,使B1M=2BM,连接MN,连接BC1,
∵N、E为所在棱的中点,B1M=2BM,CF=2FC1
∴四边形MNFE为平行四边形,∴MN∥EF
∴A1N∥AE,又A1N∩MN=N,∴平面A1MN∥平面AEF,
∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
则P必在线段MN上,AM=$\frac{\sqrt{13}}{3}$,AN=$\frac{\sqrt{5}}{2}$,MN=$\frac{5}{6}$'
在△A1MN中,由余弦定理求得cos∠MA1N=$\frac{6}{\sqrt{65}}$,⇒sin∠MA1N=$\frac{\sqrt{29}}{\sqrt{65}}$.
由面积相等得MN•h=A1M•A1Nsin∠MA1N⇒h=$\frac{\sqrt{29}}{5}$,
则线段A1P长度的取值范围是[$\frac{\sqrt{29}}{5},\frac{\sqrt{13}}{3}$]
故选:B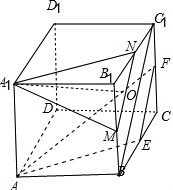
点评 本题考查点、线、面间的距离问题,考查学生的运算能力及推理转化能力,属中档题,解决本题的关键是通过构造平行平面寻找P点位置.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
13.若数列{an}的前n项和为Sn=kn2+n,且a10=39,则a100=( )
| A. | 200 | B. | 199 | C. | 299 | D. | 399 |
3.已知四组函数:
①f(x)=x,g(x)=($\sqrt{x}$)2;
②f(x)=x,g(x)=$\root{3}{{x}^{3}}$;
③f(n)=2n-1,g(n)=2n+1(n∈N);
④f(x)=x2-2x-1,g(t)=t2-2t-1.
其中是同一函数的( )
①f(x)=x,g(x)=($\sqrt{x}$)2;
②f(x)=x,g(x)=$\root{3}{{x}^{3}}$;
③f(n)=2n-1,g(n)=2n+1(n∈N);
④f(x)=x2-2x-1,g(t)=t2-2t-1.
其中是同一函数的( )
| A. | 没有 | B. | 仅有② | C. | ②④ | D. | ②③④ |
7.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①5,9,100,107,111,121,180,195,200,265,
②7,34,61,88,115,142,169,196,223,250;
③30,57,84,111,138,165,192,219,246,270;
④11,38,65,92,119,146,173,200,227,254;
关于上述样本的下列结论中,正确的是( )
①5,9,100,107,111,121,180,195,200,265,
②7,34,61,88,115,142,169,196,223,250;
③30,57,84,111,138,165,192,219,246,270;
④11,38,65,92,119,146,173,200,227,254;
关于上述样本的下列结论中,正确的是( )
| A. | ②、④都可能为分层抽样 | B. | ①、③都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ②、③都不能为系统抽样 |