题目内容
在边长为3的等边三角形ABC中,点P在边AB上,
=λ
,
•
=1,则实数λ的值是 .
| AP |
| PB |
| PA |
| PC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得
=
•
,
=
+
,利用两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义化简
•
=1,求得λ 的值.
| PA |
| λ |
| 1+λ |
| BA |
| PC |
| PA |
| AC |
| PA |
| PC |
解答:
解:由题意可得
=
•
,
=
+
,
∴
•
=
•(
+
)=PA2+
•
=(3•
)2+3•
•3cos120°=1,
即 7λ2-13λ-2=0,求得λ=2,或λ=-
(舍去),
故答案为:2.
| PA |
| λ |
| 1+λ |
| BA |
| PC |
| PA |
| AC |
∴
| PA |
| PC |
| PA |
| PA |
| AC |
| PA |
| AC |
| λ |
| 1+λ |
| λ |
| 1+λ |
即 7λ2-13λ-2=0,求得λ=2,或λ=-
| 1 |
| 7 |
故答案为:2.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
已知实数x,y满足不等式组
,则
的取值范围是( )
|
| y+1 |
| x+2 |
| A、(-1,-2] | ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知函数f(x)=sin(2x+φ),其中φ为实数,且f(x)≤f(
)对x∈R恒成立.记P=f(
),Q=f(
),R=f(
),则P,Q,R的大小关系是( )
| 2π |
| 9 |
| 2π |
| 3 |
| 5π |
| 6 |
| 7π |
| 6 |
| A、R<P<Q |
| B、Q<R<P |
| C、P<Q<R |
| D、Q<P<R |
边长为2的正三角形的顶点和各边的中点共6个点,从中任选两点,所选出的两点之间距离大于1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
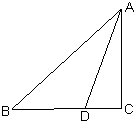 如图,在Rt△ABC(C为直角)中,D为BC边上的一个三等分点(靠近点C),则tan∠BAD的最大值为
如图,在Rt△ABC(C为直角)中,D为BC边上的一个三等分点(靠近点C),则tan∠BAD的最大值为