题目内容
边长为2的正三角形的顶点和各边的中点共6个点,从中任选两点,所选出的两点之间距离大于1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:从6个点中选出2个的选法共有∁62=15种,若使得取出的两点中距离为2,则只能是三角形的顶点中任意取出2个,只有3种情况,每个边的中点到对着的顶点的距离也大于1,代入古典概率的求解公式即可求解
解答:
解:从6个点中选出2个的选法共有∁62=15种
若使得取出的两点中距离为2,则只能是三角形的顶点中任意取出2个,只有3种情况,
每个边的中点到对着的顶点的距离也大于1,有3种情况,
故由古典概型概率公式:
=
,
故选C.
若使得取出的两点中距离为2,则只能是三角形的顶点中任意取出2个,只有3种情况,
每个边的中点到对着的顶点的距离也大于1,有3种情况,
故由古典概型概率公式:
| 3+3 |
| 15 |
| 2 |
| 5 |
故选C.
点评:本题主要考查了古典概率的计算公式的应用,属于基础试题

练习册系列答案
相关题目
已知三个数1,m,4成等比数列,则圆锥曲线x2+
=1的离心率为 ( )
| y2 |
| m |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知实数x,y满足条件
,那么目标函数z=x+2y的最小值是( )
|
| A、-6 | B、-4 | C、-2 | D、4 |
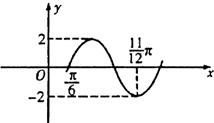 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<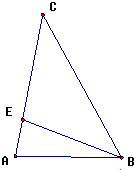 已知在△ABC中,A、B、C成等差数列,
已知在△ABC中,A、B、C成等差数列,