题目内容
一个盒子中装有4张卡片,每张卡片上写有一个数字,数字分别是1,2,3,4,现从盒子中随机抽取卡片.
(I)若一次从中随机抽取3张卡片,求3张卡片上数字之和不小于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,其上面数字记为a,放回后再随机抽取1张卡片,其上面数字记为b,求关于x的方程x2+2ax+b2=0有实数根的概率.
(I)若一次从中随机抽取3张卡片,求3张卡片上数字之和不小于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,其上面数字记为a,放回后再随机抽取1张卡片,其上面数字记为b,求关于x的方程x2+2ax+b2=0有实数根的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)由题意知本题是一个古典概型,试验包含的所有事件是任取三张卡片,三张卡片上的数字全部可能的结果,可以列举出,而满足条件的事件数字之和大于7的,可以从列举出的结果中看出.
(Ⅱ)设事件B表示“关于x的方程x2+2ax+b2=0有实数根”,则判别式△=4a2-4b2≥0,又a>0,b>0,所以a≥b,由此得到基本事件以及满足条件的事件个数,由古典概型概率公式解答.
(Ⅱ)设事件B表示“关于x的方程x2+2ax+b2=0有实数根”,则判别式△=4a2-4b2≥0,又a>0,b>0,所以a≥b,由此得到基本事件以及满足条件的事件个数,由古典概型概率公式解答.
解答:
解:(Ⅰ)由题意知本题是一个古典概型,
设A表示事件“抽取3张卡片上的数字之和不小于7”,
∵任取三张卡片,三张卡片上的数字全部可能的结果是(1、2、3),(1、2、4),(1、3、4),(2、3、4),
其中数字之和不小于7的是(1、2、4),(1、3、4),(2、3、4),
∴P(A)=
.
(Ⅱ)设事件B表示“关于x的方程x2+2ax+b2=0有实数根”,则判别式△=4a2-4b2≥0,又a>0,b>0,所以a≥b,由题意,基本事件有:(1,1),(1,2),(1,3),(1,4),(2,1)(2,2)(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共有16个,其中第一个数为a,第二个数为b,则事件B 包含10个事件,所以事件B发生的概率为
=
.
设A表示事件“抽取3张卡片上的数字之和不小于7”,
∵任取三张卡片,三张卡片上的数字全部可能的结果是(1、2、3),(1、2、4),(1、3、4),(2、3、4),
其中数字之和不小于7的是(1、2、4),(1、3、4),(2、3、4),
∴P(A)=
| 3 |
| 4 |
(Ⅱ)设事件B表示“关于x的方程x2+2ax+b2=0有实数根”,则判别式△=4a2-4b2≥0,又a>0,b>0,所以a≥b,由题意,基本事件有:(1,1),(1,2),(1,3),(1,4),(2,1)(2,2)(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共有16个,其中第一个数为a,第二个数为b,则事件B 包含10个事件,所以事件B发生的概率为
| 10 |
| 16 |
| 5 |
| 8 |
点评:古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件,概率问题同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
函数y=esinx(π≤x≤π)的图象大致为( )
A、 |
B、 |
C、 |
D、 |
一个几何体的三视图如图所示,则该几何体的体积、表面积为( )

A、π+
| ||||||||
B、2π+
| ||||||||
C、π+
| ||||||||
D、2π+
|
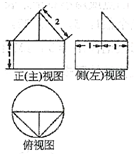
一个棱锥的三视图如图,则该棱锥的体积是( )


A、
| ||
B、
| ||
| C、4 | ||
| D、8 |

 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为