题目内容
过椭圆
+
=1的左焦点F(-
,0)作两条互相垂直的直线与椭圆分别相交于A、C及B、D,当直线AC与x轴垂直时,四边形ABCD的面积为4.
(Ⅰ)求椭圆标准方程;
(Ⅱ)求
的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆标准方程;
(Ⅱ)求
| |AC|2|BD|2 |
| |AC|+|BD| |
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出AC与x轴垂直时的弦长,求出四边形的面积,解得b,再由a,b,c的关系,即可得到椭圆方程;
(Ⅱ)由于直线AC,BD均过左焦点,则以左焦点为极点,x轴为极轴,建立极坐标系,则有ρ=
,求出弦长AC,BD,|AC|+|BD|,运用诱导公式和同角公式及二倍角公式,结合正弦函数的值域,即可得到最小值.
(Ⅱ)由于直线AC,BD均过左焦点,则以左焦点为极点,x轴为极轴,建立极坐标系,则有ρ=
| ep |
| 1-ecosθ |
解答:
解:(Ⅰ)令x=-c,则
+
=1,
则y=±
,则AC=
,
当直线AC与x轴垂直时,四边形ABCD的面积为4,
则
•
•2a=4,解得,b2=2,
又c=
,则a=
=2,
则椭圆标准方程为:
+
=1;
(2)由于直线AC,BD均过左焦点,则以左焦点为极点,x轴为极轴,建立极坐标系,
则有ρ=
=
=
=
,
则|AC|=
+
=
=
,
则有|BD|=
=
,
即有|AC|+|BD|=
+
=
,
则
=
•
,
由于(1-
sin2θ)(1-
cos2θ)=1-
(sin2θ+cos2θ)+
sin2θcos2θ
=
+
(sin2θ)2,
当sin2θ=±1时,上式取得最大值,且为
+
=
.
则有
的最小值为
×
=
.
| c2 |
| a2 |
| y2 |
| b2 |
则y=±
| b2 |
| a |
| 2b2 |
| a |
当直线AC与x轴垂直时,四边形ABCD的面积为4,
则
| 1 |
| 2 |
| 2b2 |
| a |
又c=
| 2 |
| b2+c2 |
则椭圆标准方程为:
| x2 |
| 4 |
| y2 |
| 2 |
(2)由于直线AC,BD均过左焦点,则以左焦点为极点,x轴为极轴,建立极坐标系,
则有ρ=
| ep |
| 1-ecosθ |
| ||||
1-
|
| ||||||||
1-
|
| 1 | ||||
1-
|
则|AC|=
| 1 | ||||
1-
|
| 1 | ||||
1-
|
| 2 | ||||||||
(1-
|
=
| 2 | ||
1-
|
则有|BD|=
| 2 | ||
1-
|
| 2 | ||
1-
|
即有|AC|+|BD|=
| 2 | ||
1-
|
| 2 | ||
1-
|
| 3 | ||||
(1-
|
则
| |AC|2|BD|2 |
| |AC|+|BD| |
| 16 |
| 3 |
| 1 | ||||
(1-
|
由于(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 1 |
| 2 |
| 1 |
| 16 |
当sin2θ=±1时,上式取得最大值,且为
| 1 |
| 2 |
| 1 |
| 16 |
| 9 |
| 16 |
则有
| |AC|2|BD|2 |
| |AC|+|BD| |
| 16 |
| 3 |
| 16 |
| 9 |
| 256 |
| 27 |
点评:本题考查椭圆的方程和性质,考查椭圆的极坐标方程和运用:求弦长,考查三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
相关题目
如果等比数列{an}的首项、公比之和为1且首项是公比的2倍,那么它的前n项的和为( )
A、
| ||||
B、1-(
| ||||
C、1-
| ||||
D、1-
|
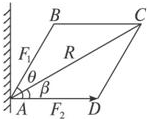 如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.
如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.