题目内容
已知三个非空集合M={x|x2-8x+k＜0}，N={x|x2-4x+3＜0}，P={x|x2-10x+16＜0}满足：若a∈M，则a∈N∪P，则k的取值范围是 ．
考点：元素与集合关系的判断
专题：集合
分析：本题可以先根据已知条件集合N、P，求出它们的交集N∪P，再利用“若a∈M，则a∈N∪P”得到集合M与N∪P的关系，对不等式x2-8x+k＜0进行研究，得到本题答案．
解答：
解：∵N={x|x2-4x+3＜0}，P={x|x2-10x+16＜0}，
∴N={x|1＜x＜3}，P={x|2＜x＜8}，
∴N∪P={x|1＜x＜8}．
∵当a∈M时，有a∈N∪P，
∴M⊆N∪P．
∵抛物线f（x）=x2-8x+k的对称轴为：x=4，
∴f（4）＜0，f（1）＞0，f（8）＞0．
∴7＜k＜16．
故答案为：（7，16）．
∴N={x|1＜x＜3}，P={x|2＜x＜8}，
∴N∪P={x|1＜x＜8}．
∵当a∈M时，有a∈N∪P，
∴M⊆N∪P．
∵抛物线f（x）=x2-8x+k的对称轴为：x=4，
∴f（4）＜0，f（1）＞0，f（8）＞0．
∴7＜k＜16．
故答案为：（7，16）．
点评：本题考查的是集合与集合的关系、元素与集合的关系，同时要求学生能熟悉一元二次不等式的解法，有一定的思维量和计算量，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
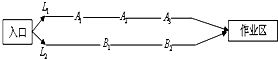某煤矿发生透水事故时，作业区有若干人员被困．救援队从入口进入之后有L1，L2两条巷道通往作业区（如图），L1巷道有A1，A2，A3三个易堵塞点，各点被堵塞的概率都是