题目内容
10.在区间〔-3,3〕上随机选取一个数x,则|x|≤1的概率为( )| A. | $\frac{1}{\begin{array}{l}3\end{array}}$ | B. | $\frac{2}{\begin{array}{l}3\end{array}}$ | C. | $\frac{1}{\begin{array}{l}4\end{array}}$ | D. | $\frac{1}{2}$ |
分析 由|x|≤1得-1≤x≤1,根据几何概型的概率公式进行求解即可.
解答 解:∵|x|≤1,
∴-1≤x≤1,
则在区间〔-3,3〕上随机选取一个数x,则|x|≤1的概率P=$\frac{1-(-1)}{3-(-3)}=\frac{2}{6}$=$\frac{1}{\begin{array}{l}3\end{array}}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设P是△ABC内一点,且$\overrightarrow{AP}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$,$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$+$\overrightarrow{AP}$=( )
| A. | $\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\frac{4}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AC}$ |
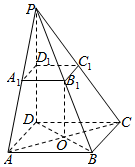 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.