题目内容
19.设P是△ABC内一点,且$\overrightarrow{AP}$+$\overrightarrow{BP}$+$\overrightarrow{CP}$=$\overrightarrow{0}$,$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$,则$\overrightarrow{AD}$+$\overrightarrow{AP}$=( )| A. | $\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\frac{4}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AC}$ |
分析 根据向量加减运算的几何意义用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AD},\overrightarrow{AP}$.
解答 解:∵$\overrightarrow{BP}=\overrightarrow{AP}-\overrightarrow{AB}$,$\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}$,$\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\overrightarrow{0}$,
∴3$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{AC}$,即$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$.
∵$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{AC}$.
∴$\overrightarrow{AD}+\overrightarrow{AP}$=$\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$.
故选:A.
点评 本题考查了平面向量线性运算的几何意义,属于中档题.

| A. | $\frac{1}{\begin{array}{l}3\end{array}}$ | B. | $\frac{2}{\begin{array}{l}3\end{array}}$ | C. | $\frac{1}{\begin{array}{l}4\end{array}}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4029}{4031}$ |
| A. | -i | B. | i | C. | 2 | D. | 1 |
| A. | -1-i | B. | 1-i | C. | 1+i | D. | -1+i |
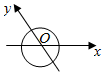 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.