题目内容
15.已知$f(x)=\left\{\begin{array}{l}|{{{log}_3}x}|,0<x≤3\\ \frac{1}{3}{x^2}-\frac{10}{3}x+8,x>3\end{array}\right.,a,b,c,d$是互不相同的正数,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是(21,24).分析 先画出函数f(x)的图象,再根据条件利用对数函数的运算性质以及指数函数的对称性,利用数形结合,即可求出其范围.
解答 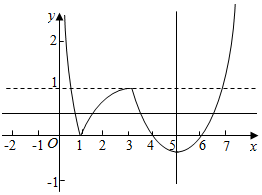 解:函数f(x)的图象如下图所示
解:函数f(x)的图象如下图所示
若a、b、c、d互不相同,且f(a)=f(b)=f(c)=f(d),
不妨令a<b<c<d,
则0<a<1,1<b<4,
则log3a=-log3b,即log3a+log3b=log3ab=0,
则ab=1,
由$\frac{1}{3}$x2-$\frac{10}{3}$x+8=1得x2-10x+21=0,
得x=7或x=3,
同时c∈(3,4),d∈(6,7),
∵c,d关于x=5对称,∴$\frac{c+d}{2}$=5,
则c+d=10,则10=c+d,
同时cd=c(10-c)=-c2+10c=-(c-5)2+25,
∵c∈(3,4),
∴当c=3时,cd=3×7=21,
当c=4时,cd=4×6=24,
∴cd∈(21,24),
即abcd=cd∈(21,24),
故答案为:(21,24);
点评 本题考查的知识点是分段函数的应用,由题意正确画出图象和熟练掌握对数函数的图象是解题的关键.利用对数函数的运算性质以及指数函数的对称性转化为一元二次函数是解决本题的关键.

练习册系列答案
相关题目
5.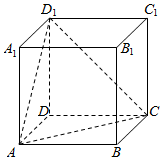 如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )
如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )
如图所示,在正方体ABCD-A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1,则tan∠DMD1的最大值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
10.在区间〔-3,3〕上随机选取一个数x,则|x|≤1的概率为( )
| A. | $\frac{1}{\begin{array}{l}3\end{array}}$ | B. | $\frac{2}{\begin{array}{l}3\end{array}}$ | C. | $\frac{1}{\begin{array}{l}4\end{array}}$ | D. | $\frac{1}{2}$ |
4.已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2015的值为( )
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4029}{4031}$ |
5.设集合A={x|x≤1},B={x|x>a},且A∩B=∅,则实数a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
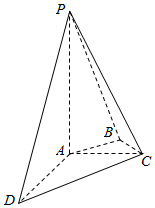 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,AD=2,AC=1,直线PA与平面PCD所成的角的正弦值为$\frac{{\sqrt{6}}}{6}$.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,AD=2,AC=1,直线PA与平面PCD所成的角的正弦值为$\frac{{\sqrt{6}}}{6}$.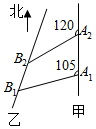 如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?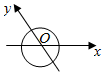 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.