题目内容

已知函数y=（m-1）x2+（m-2）x-1有两个零点，则实数m的取值范围
 
．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：根据函数零点等价于方程的根的问题，问题得以解决．
解答： 解：函数y=（m-1）x2+（m-2）x-1有两个零点，
∴（m-1）x2+（m-2）x-1=0，有两个根，
∴m≠1，且△=（m-2）2+4（m-1）＞0，
即m2＞0，且m≠1，
故实数m的取值范围为（-∞，0）∪（0，1）∪（1，+∞）
故答案为：（-∞，0）∪（0，1）∪（1，+∞）
点评：本题主要考查了函数零点与方程根的关系，属于基础题．
练习册系列答案
相关题目
函数y=x2+ax+a2-1的图象与x轴的交点分布于原点的同侧，求a的取值范围．
设函数f（x）=alnx+
1
2
x2-（a+1）x（a∈R），区间I是函数f（x）减少的区间，区间I=（α，β）（α＞β）的长度定义为β-α，记为|I|．
（1）若|I|≤1时，求实数a的取值范围；
（2）若|I|≥2，求y=|f（x）|区间[2，e2]上的最大值．（参考数据：ln3≈1.099，e2≈7.389）
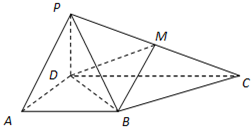如图，四棱锥P-ABCD中，底面ABCD为梯形，∠DAB=60°，AB∥CD，AD=CD=2AB，PD⊥底面ABCD，M为PC的中点．
（Ⅰ）证明：BD⊥PC；
（Ⅱ）若PD=
1
2
AD，求二面角D-BM-P的余弦值．
已知二次函数f（x）=ax2+bx（a，b为常数，a≠0）的对称轴为直线x=-1，且方程f（x）+x=0有等根．
（1）求f（x）的解析式；
（2）是否存在实数m，n（m＜n），使x∈[m，n]时，函数f（x）的最大值为3n、最小值为3m，如果存在，求出 m、n的值；如果不存在，说明理由．
已知函数f（x）满足：
①定义域为R；
②?x∈R，有f（x+2）=2f（x）；
③当x∈（0，2）时，f（x）=2-|2x-2|，设ρ（x）=f（x）-log2|x|（x∈（-8，0）∪（0，8））．
根据以上信息，可以得到函数ρ（x）的零点个数为
 
．
若不等式2x-1＞m（x2-1）对-
1
2
≤x≤
1
2
都成立，求m的取值范围．
已知x、y∈R，且x2+y2=2，求x+y的取值范围．
当函数y=x•2x取极小值时，x=（　　）
A、
1
ln2
B、-
1
ln2
C、-ln2
D、ln2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网