题目内容
8．对大于或等于2的自然数m的n次方幂有如下分解式：22=1+3，32=1+3+5，42=1+3+5+7；23=3+5，33=7+9+11，43=13+15+17+19．根据上述分解规律52=1+3+5+7+9，则53的分解中最大的数是29．
分析 由由23=3+5，33=7+9+11，43=13+15+17+19，可得53=21+23+25+27+29，问题得以解决
解答 解：由23=3+5，33=7+9+11，43=13+15+17+19，
可得53=21+23+25+27+29，
故53的分解中最大的数是29，
故答案为29
点评 本题考查归纳推理，求解的关键是根据归纳推理的原理归纳出结论，其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19．角α的终边在第三象限，那么$\frac{α}{3}$的终边不可能在的象限是第（ ）象限．
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
3．因为指数函数y=ax是增函数，而y=（$\frac{1}{2}$）x是指数函数，所以y=（$\frac{1}{2}$）x是增函数关于上面推理正确的说法是（ ）
| A． | 推理的形式错误 | B． | 大前提是错误的 | C． | 小前提是错误的 | D． | 结论是正确的 |
13．
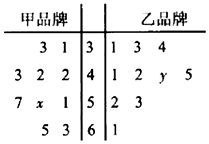某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动，为调查这100天的日销售情况，用简单随机抽样抽取10天进行统计，以它们的销售数量（单位：件）作为样本，样本数据的茎叶图如图．已知该样本中，甲品牌牛奶销量的平均数为48件，乙品牌牛奶销量的中位数为43件，将日销量不低于50件的日期称为“畅销日”．
（1）求出x，y的值；
（2）以10天的销量为样本，估计100天的销量，请完成这两种品牌100天销量的2×2列联表，并判断是否有99%的把握认为品牌与“畅销日”天数相关．
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动，为调查这100天的日销售情况，用简单随机抽样抽取10天进行统计，以它们的销售数量（单位：件）作为样本，样本数据的茎叶图如图．已知该样本中，甲品牌牛奶销量的平均数为48件，乙品牌牛奶销量的中位数为43件，将日销量不低于50件的日期称为“畅销日”．（1）求出x，y的值；
（2）以10天的销量为样本，估计100天的销量，请完成这两种品牌100天销量的2×2列联表，并判断是否有99%的把握认为品牌与“畅销日”天数相关．
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲 | 50 | 50 | 100 |
| 乙 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
20．独立性检验中，假设H0：变量X与变量Y没有关系，则在H0成立的情况下，P（K2≥6.635）≈0.010表示的意义是（ ）
| A． | 变量X与变量Y有关系的概率为1% | |
| B． | 变量X与变量Y有关系的概率为99.9% | |
| C． | 变量X与变量Y没有关系的概率为99% | |
| D． | 变量X与变量Y有关系的概率为99% |