题目内容
关于空间向量的命题:
①方向不同的两个向量不可能是共线向量;
②长度相等,方向相同的向量是相等向量;
③平行且模相等的两个向量是相等向量;
④若
≠
,则|
|≠|
|.
其中所有真命题的序号有 .
①方向不同的两个向量不可能是共线向量;
②长度相等,方向相同的向量是相等向量;
③平行且模相等的两个向量是相等向量;
④若
| a |
| b |
| a |
| b |
其中所有真命题的序号有
考点:空间向量的概念
专题:空间向量及应用
分析:①例如同一条直线上方向相反的两个单位向量是共线向量;
②利用相等向量的定义即可得出;
③平行且模相等的两个向量是相等向量或相反向量;
④不正确,例如
=-
,而|
|=|-
|.
②利用相等向量的定义即可得出;
③平行且模相等的两个向量是相等向量或相反向量;
④不正确,例如
| a |
| b |
| a |
| b |
解答:
解:①例如同一条直线上方向相反的两个单位向量是共线向量,因此不正确;
②长度相等,方向相同的向量是相等向量,正确;
③平行且模相等的两个向量是相等向量或相反向量;
④若
≠
,则|
|≠|
|,不正确,例如
=-
,而|
|=|-
|.
其中所有真命题的序号为 ②.
故答案为:②.
②长度相等,方向相同的向量是相等向量,正确;
③平行且模相等的两个向量是相等向量或相反向量;
④若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
其中所有真命题的序号为 ②.
故答案为:②.
点评:本题考查了共线向量、相等向量、模相等的向量,考查了推理能力,属于基础题.

练习册系列答案
相关题目
设a=20.1,b=ln2,c=log3
,则( )
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
sin(-
)的值等于( )
| 21π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知复数(2-i)z=1+2i,
是z的共轭复数,则
等于( )
. |
| z |
. |
| z |
| A、1 | B、i | C、-1 | D、-i |
|2x+2|-|2x-2|≤a恒成立,则实数a的取值范围是( )
| A、(-∞,-4) |
| B、[4,+∞) |
| C、[-4,+∞) |
| D、(-4,+∞) |
某几何体的三视图如图所示,它的体积为( )


| A、81π | B、57π |
| C、45π | D、12π |
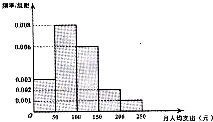 如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )
如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )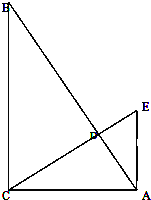 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.