题目内容
已知动圆M与圆C1:(x+3)2+y2=9外切且与圆C2:(x-3)2+y2=1内切,则动圆圆心M的轨迹方程是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:找出两圆圆心坐标与半径,设设动圆圆心M(x,y),半径为r,根据动圆M与圆C1外切且与圆C2内切,即可确定出M轨迹方程.
解答:
解:由圆C1:(x+3)2+y2=9,圆心C1(-3,0),半径r1=3,圆C2:(x-3)2+y2=1,圆心C2(3,0),r2=1,
设动圆圆心M(x,y),半径为r,
根据题意得:
,
整理得:|MC1|-|MC2|=4,
则动点M轨迹为双曲线,a=2,b=
,c=3,其方程为
-
=1(x≥2).
故答案为:
-
=1(x≥2)
设动圆圆心M(x,y),半径为r,
根据题意得:
|
整理得:|MC1|-|MC2|=4,
则动点M轨迹为双曲线,a=2,b=
| 5 |
| x2 |
| 4 |
| y2 |
| 5 |
故答案为:
| x2 |
| 4 |
| y2 |
| 5 |
点评:此题考查了直线与圆的位置关系,以及动点轨迹方程,熟练掌握双曲线定义是解本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
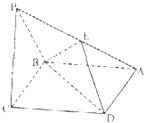 己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.
己知如图,四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°.又PC⊥平面ABCD,PC=a.E为PA的中点.