题目内容
在边长为1的正三角形ABC中,
=x
,
=y
,x>0,y>0,且x+y=1,求
•
的最大值.
| BD |
| BA |
| CE |
| CA |
| CD |
| BE |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:建立平面直角坐标系,确定A,B,C的坐标,设点D,E坐标,由
=x
,
=y
,x>0,y>0,且x+y=1,计算
•
的值即可.
| BD |
| BA |
| CE |
| CA |
| CD |
| BE |
解答:
解:建立如图所示的平面直角坐标系,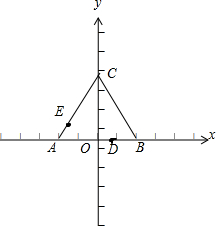
则点A(-
,0),B(
,0),C(0,
);
设点D(x1,0),E(x2,y2),∵
=x
,x>0,y>0,且x+y=1,
∴(x1-
,0)=x(-1,0),∴x1=-x+
;
∵
=y
,∴(x2,y2-
)=y(-
,-
),∴x2=-
y,y2=
-
y;
∴
•
=(x1,-
)•(x2-
,y2)=x1(x2-
)-
y2=(-x+
)•(-
y-
)-
(
-
y)
=
xy+
(x+y)-1≤
•
-
=-
,当且仅当x=y=
时取“=”;
故答案为:-
.
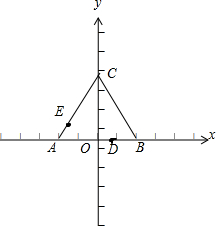
则点A(-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
设点D(x1,0),E(x2,y2),∵
| BD |
| BA |
∴(x1-
| 1 |
| 2 |
| 1 |
| 2 |
∵
| CE |
| CA |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| CD |
| BE |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
故答案为:-
| 3 |
| 8 |
点评:本题考查了平面向量的坐标表示与数量积的运算性质和向量问题的基本解法,解题时要注意向量运算与数的运算区别.

练习册系列答案
相关题目
