题目内容
若f（θ）=
+
（θ≠
，k∈Z），则f（θ）的最小值为 ．
| 2 |
| sin2θ |
| 1 |
| cos2θ |
| kπ |
| 2 |
考点：三角函数中的恒等变换应用,三角函数的最值
专题：三角函数的求值
分析：首先利用三角恒等式sin2θ+cos2θ=1对f（θ）进行恒等变换，然后使用均值不等式求的结果．
解答：
解：
∵sin2θ+cos2θ=1
∴f（θ）=
+
=
+
=3+（
+
）
∵θ≠
，k∈Z
∴
+
≥2
∴f（θ）≥3+2
故答案为：3+2
∵sin2θ+cos2θ=1
∴f（θ）=
| 2 |
| sin2θ |
| 1 |
| cos2θ |
| 2sin2θ+2cos2θ |
| sin2θ |
| sin2θ+cos2θ |
| cos2θ |
| 2cos2θ |
| sin2θ |
| sin2θ |
| cos2θ |
∵θ≠
| kπ |
| 2 |
∴
| 2cos2θ |
| sin2θ |
| sin2θ |
| cos2θ |
| 2 |
∴f（θ）≥3+2
| 2 |
故答案为：3+2
| 2 |
点评：本题考查的知识点：三角函数式的恒等变换及均值不等式．
练习册系列答案
相关题目
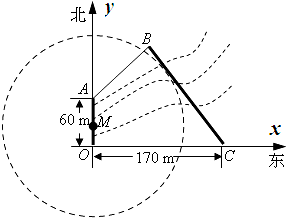如图：为了保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸）．规划要求：新桥BC与河岸AB垂直，保护区的边界为圆心M（在线段OA上）与BC相切的圆．建立如图所示的直角坐标系，已知新桥BC所在直线的方程为：4x+3y-680=0．