题目内容
19．已知a+b＞0，b=4a，（a+b）n的展开式按a的降幂排列，其中第n 项与第n+1项相等，那么正整数n等于（ ）| A． | 4 | B． | 9 | C． | 10 | D． | 11 |
分析 由题意利用二项展开式的通项公式，可得${C}_{n}^{n-1}$•a•bn-1=${C}_{n}^{n}$•bn，由此求得正整数n的值．
解答 解：∵a+b＞0，b=4a，（a+b）n的展开式按a的降幂排列，其中第n 项与第n+1项相等，
∴${C}_{n}^{n-1}$•a•bn-1=${C}_{n}^{n}$•bn，即 na•（4a）n-1=（4a）n，解得n=4，
故选：A．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
10．已知角α的终边与单位圆相交于点$P（{{{\frac{4}{5}}_{\;}}，-\frac{3}{5}}）$，现将角α的终边绕坐标原点沿逆时针方向旋转$\frac{π}{3}$，所得射线与单位圆相交于点Q，则点Q的横坐标为（ ）
| A． | $\frac{{4+3\sqrt{3}}}{10}$ | B． | $\frac{{4-3\sqrt{3}}}{10}$ | C． | $\frac{{3+4\sqrt{3}}}{10}$ | D． | $\frac{{4\sqrt{3}-3}}{10}$ |
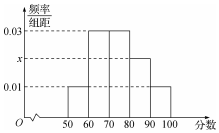2017高考特别强调了要增加对数学文化的考查，为此某校高三年级特命制了一套与数学文化有关的专题训练卷（文、理科试卷满分均为100分），并对整个高三年级的学生进行了测试．现从这些学生中随机抽取了50名学生的成绩，按照成绩为[50，60），[60，70），…，[90，100]分成了5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）．