题目内容
16.实数x,y满足$\left\{\begin{array}{l}{x≥a}\\{y≥x}\\{x+y≤2}\end{array}\right.$(a<1),且z=2x+y的最大值是最小值的4倍,则a的值是( )| A. | $\frac{2}{11}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{11}{2}$ |
分析 作出不等式组对应的平面区域,利用z的几何意义,结合目标函数z=2x+y的最大值是最小值的4倍,建立方程关系,即可得到结论.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线的截距最大,
此时z最大,
由$\left\{\begin{array}{l}{x+y=2}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$
即A(1,1),此时z=2×1+1=3,
当直线y=-2x+z经过点B时,直线的截距最小,
此时z最小,
由$\left\{\begin{array}{l}{x=a}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=a}\\{y=a}\end{array}\right.$,
即B(a,a),此时z=2×a+a=3a,
∵目标函数z=2x+y的最大值是最小值的4倍,
∴3=4×3a,
即a=$\frac{1}{4}$.
故选:B.
点评 本题主要考查线性规划的应用,利用数形结合结合目标函数的几何意义求出最优解是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
5.若点A(2,-4),点B(-2,-5),则向量$\overrightarrow{AB}$的坐标为( )
| A. | (-4,-1) | B. | (4,1) | C. | (0,-9) | D. | (-2,-5) |
8.已知$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$,且$\overrightarrow{AC}=\overrightarrow a$,$\overrightarrow{BD}=\overrightarrow b$,则$\overrightarrow{AB}$=( )
| A. | $\frac{1}{2}(\overrightarrow a-\overrightarrow b)$ | B. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | C. | $\frac{1}{2}(\overrightarrow b-\overrightarrow a)$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
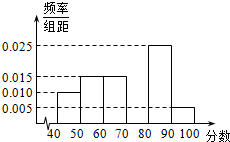 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题: