题目内容
设l、m、n是互不重合的直线,α、β是不重合的平面,则下列命题为真命题的是( )
| A、若l⊥α,l∥β,则α⊥β |
| B、若α⊥β,l?α,则l⊥β |
| C、若l⊥n,m⊥n,则l∥m |
| D、若α⊥β,l?α,n?β则l⊥n |
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:A.利用线面平行的性质定理、面面垂直的判定定理即可判断出;
B.由α⊥β,l?α,推不出l⊥β;
C.由l⊥n,m⊥n,可得l∥m、相交或为异面直线都有可能;
D.由α⊥β,l?α,n?β,可得l∥n、相交或为异面直线都有可能.
B.由α⊥β,l?α,推不出l⊥β;
C.由l⊥n,m⊥n,可得l∥m、相交或为异面直线都有可能;
D.由α⊥β,l?α,n?β,可得l∥n、相交或为异面直线都有可能.
解答:
解:A.由l⊥α,l∥β,利用线面平行的性质定理、面面垂直的判定定理可得α⊥β;
B.由α⊥β,l?α,不一定l⊥β,不正确;
C.由l⊥n,m⊥n,则l∥m、相交或为异面直线,不正确;
D.由α⊥β,l?α,n?β,则l∥n、相交或为异面直线,不正确.
故选:A.
B.由α⊥β,l?α,不一定l⊥β,不正确;
C.由l⊥n,m⊥n,则l∥m、相交或为异面直线,不正确;
D.由α⊥β,l?α,n?β,则l∥n、相交或为异面直线,不正确.
故选:A.
点评:本题考查了空间位置关系的判定、简易逻辑的判定,考查了推理能力,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
执行如图的程序框图,那么输出的S=( )


| A、720 | B、120 |
| C、24 | D、-120 |
已知三个函数f(x)=2+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则( )
| A、a<b<c |
| B、a<c<b |
| C、b<a<c |
| D、c<a<b |
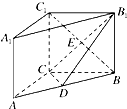 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是线段AB上的一点,且∠CDB1=90°,AA1=CD,则点A1到平面B1CD的距离为
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是线段AB上的一点,且∠CDB1=90°,AA1=CD,则点A1到平面B1CD的距离为