题目内容
甲乙两人玩射击游戏,甲命中目标的概率为
,乙命中目标的概率为t,t∈(0,1),规定:每人击3次,第一次命中得4分,第二次命中得2分,第三次命中得1分,未命中得0分,甲乙命中与否相互独立
(1)求甲总得分的期望
(2)求甲命中次数比乙多,但总分比乙少的概率p(t),并求p(t)的最大值.
| 2 |
| 3 |
(1)求甲总得分的期望
(2)求甲命中次数比乙多,但总分比乙少的概率p(t),并求p(t)的最大值.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)由已知得,甲得分的X的可能取值为0,1,2,3,4,5,6,7,分别求出相应的概率,由此能求出甲总得分的期望EX.
(2)甲命中次数比乙多,但总分比乙少,甲第一次不中,后两次全中,乙第一次中,后两次全不中,由此能求出相应的概率p(t),并由导数性质能求出p(t)的最大值.
(2)甲命中次数比乙多,但总分比乙少,甲第一次不中,后两次全中,乙第一次中,后两次全不中,由此能求出相应的概率p(t),并由导数性质能求出p(t)的最大值.
解答:
解:(1)由已知得,甲得分的X的可能取值为0,1,2,3,4,5,6,7,
P(X=0)=(
)3=
,
P(X=1)=(
)2×
=
,
P(X=2)=
×
×
=
,
P(X=3)=
×
×
=
,
P(X=4)=
×
×
=
,
P(X=5)=
×
×
=
,
P(X=6)=(
)2×
=
,
P(X=7)=(
)3=
,
∴甲总得分的期望EX=0×
+1×
+2×
+3×
+5×
+6×
+7×
=
.
(2)∵甲命中次数比乙多,但总分比乙少,
∴甲第一次不中,后两次全中,乙第一次中,后两次全不中,
∴P(t)=
×(
)2×t(1-t)2=
(t3-2t2+t).
∵t∈(0,1),P(t)=
(t3-2t2+t).
∴P′(t)=
t2-
t+
,
由P′(t)=0,得t=
或t=1(舍),
t∈(0,
)时,P′(t)>0,t∈(
,1)时,P′(t)<0,
∴t=
时,[P(t)]max=P(
)=
(
-
+
)=
.
∴p(t)的最大值为
.
P(X=0)=(
| 1 |
| 3 |
| 1 |
| 27 |
P(X=1)=(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
P(X=2)=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
P(X=3)=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
P(X=4)=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
P(X=5)=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
P(X=6)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
P(X=7)=(
| 2 |
| 3 |
| 8 |
| 27 |
∴甲总得分的期望EX=0×
| 4 |
| 27 |
| 2 |
| 27 |
| 2 |
| 27 |
| 4 |
| 27 |
| 4 |
| 27 |
| 4 |
| 27 |
| 8 |
| 27 |
| 118 |
| 27 |
(2)∵甲命中次数比乙多,但总分比乙少,
∴甲第一次不中,后两次全中,乙第一次中,后两次全不中,
∴P(t)=
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
∵t∈(0,1),P(t)=
| 4 |
| 27 |
∴P′(t)=
| 4 |
| 9 |
| 16 |
| 27 |
| 4 |
| 27 |
由P′(t)=0,得t=
| 1 |
| 3 |
t∈(0,
| 1 |
| 3 |
| 1 |
| 3 |
∴t=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
| 1 |
| 27 |
| 2 |
| 9 |
| 1 |
| 3 |
| 4 |
| 81 |
∴p(t)的最大值为
| 4 |
| 81 |
点评:本题考查离散型随机变量的数学期望的求法,考查概率及概率的最大值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目

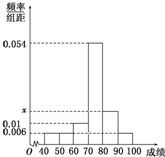 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: