题目内容
已知椭圆的中心在原点,一个焦点是(1,0),这个椭圆与直线y=x-1交于A、B两点,若以A、B为直径的圆过椭圆左焦点,求椭圆方程.
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由题意设出椭圆方程,和直线方程联立后化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横纵坐标的乘积,再结合
•
=0即可求得m的值,则椭圆方程可求.
| FA |
| FB |
解答:
解:由题意设椭圆方程为
+
=1,
联立
,得(2m-1)x2-2mx+2m-m2=0.
由根与系数关系得:x1x2=
.
以AB为直径的圆过椭圆的焦点F(-1,0),
∴
•
=0,即
(x1+1)(x2+1)+y1y2=0,
(x1+1)(x2+1)+(x1-1)(x2-1)=0.
∴x1x2=-1,
得
=-1,解得:
m=2±
.
又∵m>1
∴m=2+
.
∴椭圆方程为:
+
=1.
| x2 |
| m |
| y2 |
| m-1 |
联立
|
由根与系数关系得:x1x2=
| 2m-m2 |
| 2m-1 |
以AB为直径的圆过椭圆的焦点F(-1,0),
∴
| FA |
| FB |
(x1+1)(x2+1)+y1y2=0,
(x1+1)(x2+1)+(x1-1)(x2-1)=0.
∴x1x2=-1,
得
| 2m-m2 |
| 2m-1 |
m=2±
| 3 |
又∵m>1
∴m=2+
| 3 |
∴椭圆方程为:
| x2 | ||
2+
|
| y2 | ||
1+
|
点评:本题考查了椭圆方程的求法,考查了平面向量在解题中的应用,体现了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、命题“若x=1则x2=1”的否命题为“若x2≠1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、“命题p,q中至少有一个为真命题”是“p或q为真命题”的充分不必要条件 |

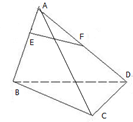 如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.
如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.